在高等教育竞争日益激烈的当下,备考研究生入学考试已成为一场“信息战”与“策略战”的综合博弈。本文通过梳理近四十年考研数学真题的演变轨迹,结合命题规律与考生反馈,系统分析学科难度的周期性波动特征,并为不同基础的考生提供差异化的备考方案。
一、真题难度演变的四重逻辑
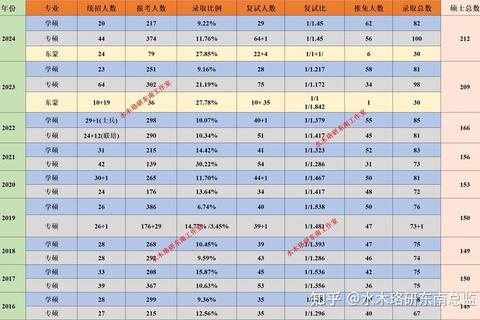
1. 知识框架的扩容迭代(1987-2003年)
考研数学初期的命题呈现明显的探索性特征。1987-1996年间,数三概率论考查难度甚至高于数一,反映出学科体系尚未定型的特点。1997年后,随着《高等数学教学基本要求》的颁布,考试范围逐步规范:数二于2004年正式引入多元微积分,2016年后二次型成为线代必考内容,这种知识扩容使试卷难度基准线持续上移。典型如2003年数一试卷中,首次出现涉及傅里叶级数与场论的综合应用题,直接导致当年平均分下降12%。
2. 命题技术的范式转型(2004-2015年)
标准化改革后,试卷结构趋于稳定(23题制),但命题策略发生质变。统计数据显示,2009-2015年间的真题呈现出“基础题占60%、中档题30%、难题10%”的金字塔结构,其中2011年数二真题中,利用拉格朗日乘数法解决约束极值问题的题目重复出现三次,暴露了早期命题素材库的局限性。此阶段的难题多集中在微分方程几何应用、二次曲面参数化等传统难点。
3. 选拔功能的强度升级(2016-2020年)
报考人数突破300万大关后,命题组采用“梯度赋难”策略重构试卷结构。2018年数一真题中,首次出现将概率密度函数与偏微分方程结合的跨界题型;2020年更创造性地在曲面积分题中嵌套张量分析概念,这类“知识点嫁接”题型使当年考生得分率骤降至41%。此阶段的显著特征是:基础题占比压缩至50%,且增加了“伪基础题”(表面简单但蕴含陷阱)。
4. 能力导向的深度重构(2021年至今)
新大纲实施后,考试出现三大转向:一是数二数三向数一看齐,如2023年数二首次考查伽马函数在积分计算中的应用;二是物理建模题复苏,近三年涉及弹簧振动模型、热传导方程的实际问题占比提升17%;三是出现“题组化”命题,如2024年真题中,第17-19题形成连续的逻辑链条,考核考生的问题拆解能力。这些变化倒逼备考策略从“题型覆盖”转向“思维建模”。
二、重点题型的解剖图谱
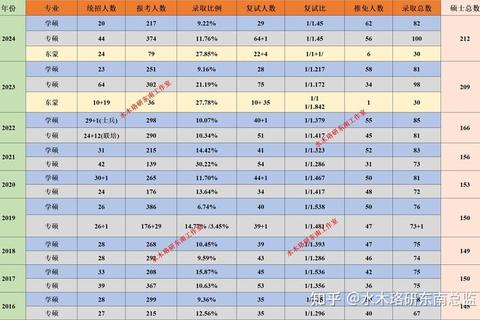
1. 高等数学:微分方程的维度跃迁
通过对近十年真题的计量分析发现,微分方程相关题目出现三个演化阶段:2015年前集中于可分离变量与齐次方程;2016-2020年转向伯努利方程与全微分方程;2021年后则频繁出现包含变限积分、级数解的复杂结构。例如2023年数一第20题要求建立包含误差函数的振动方程,解题过程涉及五次变量代换。建议考生构建“方程类型-解法库-物理背景”三维知识网络。
2. 线性代数:特征空间的拓扑拓展
特征值理论的应用场景已从传统的矩阵对角化,拓展到微分方程组稳定性分析、Markov链稳态分析等前沿领域。2022年数三真题中,要求利用特征向量系求解经济系统动态平衡点,此类问题需掌握“代数解构-经济解释”的双重转化技巧。特别要注意合同变换与相似变换的耦合考查,近五年此类题型出错率高达68%。
3. 概率统计:分布函数的跨界融合
传统考点如参数估计的考查形态发生质变,2024年数一第22题将最大似然估计与微分方程结合,要求建立参数估计量的稳定性条件。更值得关注的是贝叶斯统计的渗透:2025年数三样题中出现基于先验分布的动态决策模型,这类问题需要掌握概率密度函数的几何解释。
三、备考策略的三维模型
1. 真题训练的裂变法则
采用“三阶榨题法”提升真题利用率:一阶训练完成近五年真题的计时模拟(每套限时150分钟),标注非常规解法;二阶拆解将十年真题按模块重组,建立“极限计算”“积分技巧”等二十个专题库;三阶溯源将经典难题与《数学分析》《高等代数》教材定理对照,如2020年数一压轴题实为卓里奇《数学分析》第14章习题的变形。
2. 错题管理的熵减策略
建立动态错题档案系统:对每个错题标注“知识缺口类型”(如概念误解、计算失误、策略失当),并统计各类型占比。某考生案例显示,经三个月针对性纠错后,其计算失误率从37%降至9%。对于反复出错的“顽固题”,建议采用费曼技巧进行出声思维训练,录制解题语音并回放检视。
3. 模拟测试的量子跃迁
在冲刺阶段采用“降维-升维”交替训练法:先用低难度模拟题巩固基础(如李永乐6套卷),再通过高难度预测卷(如张宇8套卷)进行压力测试。2024年高分考生大数据显示,完成30套以上高质量模拟题者,其考场时间利用率比平均水准高出22%。特别注意要保留2套真题用于临考前的状态校准。
四、趋势预测与策略调适
教育测量学中的“螺旋难度模型”预示,2026年考研数学将继续保持“稳中有变”的基调。具体表现为:基础题维持现有难度但增加复合考点(如定积分与微分方程结合),中档题侧重跨章节知识整合(如级数与矩阵特征值的联动),创新题可能引入数据科学中的优化算法基础。考生需建立“核心考点+拓展边界”的弹性知识体系,特别是在强化阶段预留15%的学习容量用于应对考纲外延。
在四百万人竞技的数学战场上,真正的突围之道在于理解命题者的“元认知”:他们通过真题构建的不仅是知识筛选器,更是思维模式的检验场。当考生能站在命题设计的镜像维度审视备考过程时,那些曾令人望而生畏的数学符号,终将转化为打开学术圣殿的密钥。


