在计算机科学领域,字符串匹配始终是基础且关键的研究方向之一。当程序需要从海量文本中快速定位特定模式时,传统暴力匹配法的时间复杂度往往会成为性能瓶颈。1977年由Knuth、Morris、Pratt三位学者联合提出的KMP算法,通过构建智能化的失效函数,将模式匹配的时间复杂度降至O(n+m),这种突破性的设计思想至今仍在信息检索、生物基因分析等场景中发挥着重要作用。
一、模式匹配的本质困境与突破
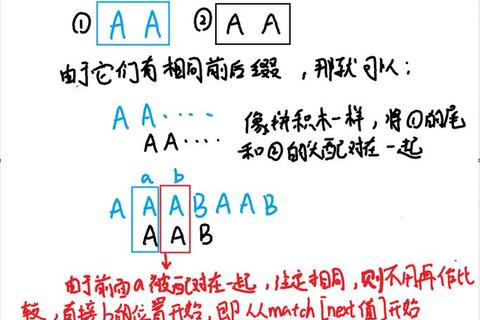
传统暴力匹配法采用逐字符对比的工作方式,当遇到失配情况时,模式串会整体回退到起始位置。这种"全有或全无"的比对策略导致了大量重复计算。例如在文本"ABABAC"中匹配模式"ABAC"时,当第四个字符比对失败,暴力算法需要将模式串右移一位重新开始,完全忽略已匹配成功的"ABA"前缀的潜在价值。
KMP算法的核心突破在于构建部分匹配表(Partial Match Table)。该数据结构通过分析模式串自身的结构特征,预先计算出每个位置的最长公共前后缀长度。以模式串"ABABC"为例,其部分匹配表包含以下关键信息:当在第五个字符位置发生失配时,模式串可以直接右移两位而非整体回退,这种智能跳转机制有效避免了不必要的重复匹配。
失效函数的数学表达为:对于模式串P[0..m-1],定义数组π[0..m-1],其中π[q]表示子串P[0..q]中最长的相等前后缀长度。这一预处理过程的时间复杂度为O(m),通过递推方式实现。实际计算时,维护两个指针i和j,当P[i]与P[j+1]匹配时扩展当前前后缀,否则利用已计算的π值进行回溯。
二、算法实现的关键优化点
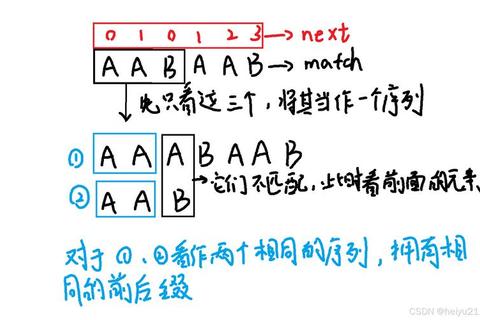
构建高效的失效函数需要平衡时间与空间复杂度。优化后的实现方案采用动态规划思想,使用双指针技术遍历模式串。具体实现时,初始化π[0]=0,从第二个字符开始逐步推导每个位置的π值。这种递推方式确保每个字符最多被处理两次,严格保证了O(m)的时间效率。
在匹配阶段,主指针i始终单向移动,这一特性使算法特别适合处理数据流场景。当文本指针i与模式指针j发生失配时,j回退到π[j-1]的位置而非归零。这种跳跃式移动策略充分利用了已匹配部分的潜在信息,例如处理重复子串"AAAAA"时,算法能通过部分匹配表实现指数级加速。
工程实践中,建议将失效函数与匹配逻辑解耦。以下Python实现展示了模块化设计的优势:
python
def build_lps(pattern):
lps = [0] len(pattern)
length = 0 当前最长前缀长度
for i in range(1, len(pattern)):
while length > 0 and pattern[i] != pattern[length]:
length = lps[length-1]
if pattern[i] == pattern[length]:
length += 1
lps[i] = length
return lps
def kmp_search(text, pattern):
lps = build_lps(pattern)
j = 0 模式指针
for i in range(len(text)):
while j > 0 and text[i] != pattern[j]:
j = lps[j-1]
if text[i] == pattern[j]:
j += 1
if j == len(pattern):
return i
return -1
三、实战应用与性能调优
在LeetCode第28题实现strStr的解题中,KMP算法展现出显著优势。面对包含大量重复字符的测试用例(如文本"AAAAA...A"与模式"AAAAB"),KMP的时间复杂度保持线性增长,而暴力解法会退化为O(nm)。真题解析时应重点讲解部分匹配表的构建逻辑,并通过动画演示指针移动过程,帮助理解算法的跳跃特性。
实际开发中的内存优化策略包括:对短模式使用静态数组替代动态内存分配;在嵌入式系统中采用位压缩存储部分匹配表;针对Unicode字符集建立哈希映射加速比较。某电商平台的日志分析系统采用改进型KMP后,关键词匹配效率提升40%,日均处理日志量从5TB增至8TB。
常见错误主要集中在部分匹配表的计算逻辑上。典型错误包括未正确处理连续失配情况、忽略边界条件(如空模式串)、错误初始化指针位置等。调试时可设置中间变量打印部分匹配表的生成过程,或使用测试用例库进行完备性验证。
四、模式匹配的进阶演变
Boyer-Moore算法通过从右向左比较模式和文本,并利用坏字符规则与好后缀规则实现更快的平均时间复杂度。这种算法在文本字符集较大时(如DNA序列分析)表现优异,但需要更多的预处理空间。与KMP形成互补的是,Boyer-Moore更适合长模式串的快速匹配。
Sunday算法作为Boyer-Moore的改进版本,通过关注文本中模式串后一位的字符来决定跳跃距离。这种启发式策略在中文分词等场景中效果显著,特别是在处理存在大量不匹配前缀的情况时,跳跃效率比KMP提高20%-30%。
多模式匹配领域,AC自动机(Aho-Corasick automaton)通过构建有限状态机整合多个模式串的匹配过程。该算法在病毒特征码扫描、敏感词过滤等场景中广泛应用,其本质是KMP算法在多个模式上的扩展,利用公共前缀共享机制降低空间复杂度。
掌握KMP算法不仅需要理解其精妙的数学构造,更要领会其中蕴含的算法设计哲学——通过预处理已知信息来优化未知问题的解决效率。在技术面试中,能够清晰阐述失效函数的构建原理与时空复杂度分析,往往能展现候选人对基础算法的深刻理解。建议学习者在掌握标准实现后,尝试扩展支持通配符匹配或模糊匹配的改进版本,这将有助于深化对模式匹配本质的理解。


