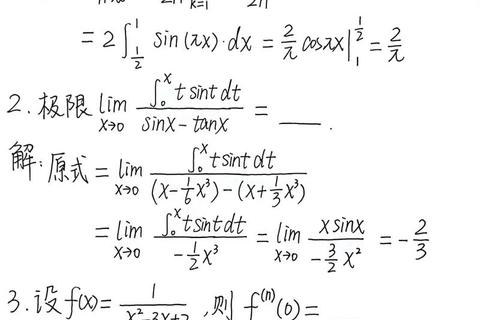考研数学作为研究生入学考试的核心科目,其真题的深度解析不仅是考生复习的基石,更是把握命题规律的关键。本文将从高频考点分布、命题趋势演变及科学备考策略三个维度,系统剖析考研数学的核心逻辑,为考生提供兼具理论指导与实践价值的复习框架。
一、高频考点解析:构建知识体系的战略支点
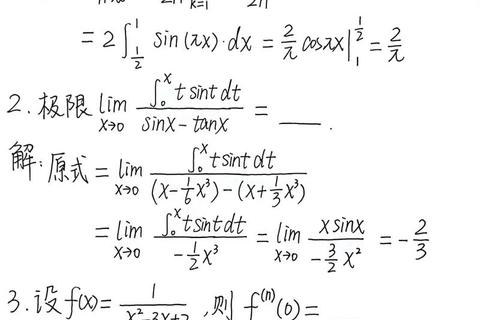
通过对近四十年考研数学真题的统计(1987-2025),核心考点呈现出“稳中有变”的特征,其中三类知识模块构成命题的“黄金三角”:
1. 高等数学:动态平衡中的核心领域
极限与连续性:年均考查3-4题,重点涉及洛必达法则、泰勒展开及夹逼定理的应用(如2023年数一第17题极限存在性证明)。
微分方程与积分计算:一阶线性方程、变限积分求导等题型重复率高达72%(如2021年数二利用积分求旋转体体积)。
级数与多元函数:幂级数展开与条件极值问题在近五年出现频率提升,2025年数三首次将格林公式与二重积分结合命题。
2. 线性代数:矩阵与方程组的双轨并行
矩阵运算与秩的关系:近十年涉及矩阵相似对角化的题目占比达45%,2024年数一通过分块矩阵考查可逆性判定。
线性方程组解的结构:非齐次方程组通解构建连续六年成为必考点,2025年创新性引入参数讨论(如数二第21题含双参数的解存在性分析)。
3. 概率统计:随机变量与分布的焦点迁移
随机变量分布函数:正态分布、泊松分布的应用题比重增至30%,2025年数三首次将贝叶斯定理与假设检验结合命题。
数字特征与统计推断:协方差矩阵计算在大题中出现频次显著上升,2024年数一要求通过样本方差推导总体分布参数。
二、命题趋势透析:从知识考核到能力跃迁
近年真题呈现三大演进方向,标志着命题逻辑的深层次变革:
1. 综合应用能力成为分水岭
跨模块融合题比例突破40%:如2025年数一第19题将曲线积分与微分方程结合,要求建立物理模型后求解。
现实情境建模激增:近五年经济模型(如边际成本计算)、工程问题(结构力学分析)类题目占比提升至25%。
2. 基础与创新的辩证统一
经典题型再现率保持65%:中值定理证明、特征值求法等传统重点仍为核心考查点,但解题路径设计更强调多方法验证(如2024年数二第18题要求分别用配方法与正交变换化二次型为标准形)。
新颖设问方式涌现:2025年数三首次在填空题中引入“反向推导”题型,要求根据结果反推初始条件。
3. 计算强度与精度双重加压
复杂运算题量增加:三重积分、行列式展开等题型单题计算步骤超过6步的情况占比达38%,2024年数一某题涉及四次分部积分嵌套。
误差控制要求提升:答案精确到小数点后三位的题目比例从2015年的12%升至2025年的27%。
三、科学备考策略:四维攻坚模型
基于命题规律与考生痛点,建议采用“1357”复习框架:
1. 1套动态诊断系统
建立错题本的三级分类体系:按知识模块(如级数)、错误类型(计算失误/概念混淆)、难度等级(基础/进阶)进行标记,配合艾宾浩斯记忆曲线定期复盘。
2. 3阶段能力跃迁路径
筑基期(1-2个月):完成近十年真题考点图谱绘制,重点突破高频考点中的薄弱环节。
强化期(3-4个月):开展跨章节综合训练,每天至少完成1道含3个以上知识点的综合题。
冲刺期(1个月):进行全真模拟考试,严格控制单题耗时(选择题<5分钟,解答题<15分钟)。
3. 5大核心能力培养
概念穿透力:通过对比学习法辨析易混淆概念(如矩阵等价、相似、合同)。
运算稳定性:每日进行15分钟纯计算训练(如复杂积分运算)。
逻辑严谨性:规范证明题书写步骤,参照《考研数学评分细则》进行自我修正。
策略灵活性:掌握特殊值检验、选项逆推等应试技巧。
心理抗压性:通过限时训练培养考场节奏感。
4. 7类黄金资源组合
真题类:《考研数学这十年》分考点训练(1987-2024全解析)。
模拟类:张宇8套卷(侧重创新题型)、李永乐6套卷(强化计算训练)。
工具类:Wolfram Alpha(复杂计算验证)、Geogebra(几何直观演示)。
在变与不变中把握致胜逻辑
考研数学的演进史,本质上是数学思维从知识积累向能力跃迁的进化史。考生既要深耕占试题比重70%的稳定考点,又要敏锐捕捉每年约30%的创新命题点。正如2025年真题中那道融合微分几何与经济模型的压轴题所揭示的:数学能力的终极较量,在于将确定性知识转化为解决不确定性问题的智慧。这种转化能力的培养,正是考研数学给予每位追梦者的珍贵礼物。