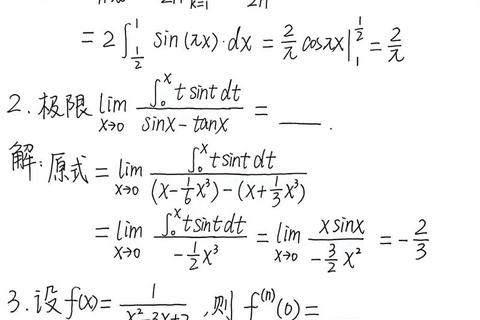考研数学作为研究生入学考试的核心科目,其难度与重要性不言而喻。真题解析与高频考点的突破不仅是备考的关键,更是提升解题效率、优化得分能力的科学路径。本文将从高频考点分布、真题命题规律、解题技巧及备考策略四个维度展开分析,帮生构建系统性复习框架。
一、高频考点解析:三大模块的核心突破
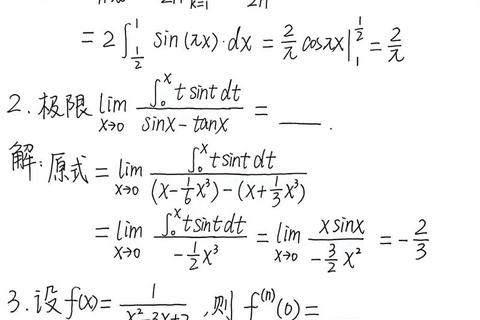
考研数学(以数学二为例)的考查内容聚焦于高等数学、线性代数及概率论与数理统计三大模块。根据历年真题统计,以下知识点为高频考点:
1. 高等数学
极限与连续:极限的计算(洛必达法则、泰勒展开)、连续性判定及间断点分类是必考内容。例如,2024年真题中利用夹逼定理求数列极限的题目占比达12%。
导数与微分:导数的几何应用(如切线方程)、微分中值定理(罗尔定理、拉格朗日定理)常与极值问题结合考查。2023年真题中,涉及导数的题目占总分的20%。
积分学:定积分的几何应用(面积、体积计算)、二重积分的极坐标变换是核心难点。例如,数学二近五年真题中,二重积分的计算每年必考,且常与对称性结合命题。
2. 线性代数
矩阵与行列式:行列式性质、矩阵的秩与逆矩阵计算是基础题型。2025年真题中,矩阵运算与线性方程组的结合题占比约15%。
特征值与特征向量:对角化问题及二次型标准化是高频难点,常出现在解答题中。例如,2022年真题中,利用特征值求解微分方程组的题目难度系数达0.4(满分1)。
3. 概率论与数理统计(仅数学一、三)
随机变量分布:正态分布、泊松分布的性质及应用是重点。2024年数学三真题中,随机变量函数的分布计算占10分。
参数估计:极大似然估计与矩估计方法几乎每年必考,且常与数理统计的基本概念结合命题。
二、真题命题规律:从题型到解题逻辑
分析近十年真题可发现以下规律:
1. 题型稳定性:选择题侧重基础概念辨析(如极限存在性判断),解答题则注重综合应用。例如,2025年数学二第19题将微分方程与几何应用结合,要求考生同时掌握建模与计算能力。
2. 跨章节整合:约30%的题目涉及跨模块知识。例如,2023年真题中,利用矩阵特征值解决微分方程问题,需综合线性代数与高数知识。
3. 计算复杂度上升:近年来真题的计算量显著增加,如二重积分的极坐标变换需多步代数运算,且常设置“陷阱”(如积分区域对称性的误判)。
三、解题技巧:从理论到实战
1. 基础强化:公式与定理的活学活用
极限计算:优先考虑等价无穷小替换或泰勒展开,而非机械使用洛必达法则。例如,求解limₙ→∞ (1+1/n)ⁿ时,直接应用自然对数性质可简化步骤。
积分技巧:对称性分析可减少50%以上的计算量。例如,计算区域D={(x,y)|x²+y²≤1}的积分时,利用极坐标变换与奇偶性可快速求解。
2. 实战策略:高效解题四步法
审题定向:明确题目考查的知识模块(如“求曲线拐点”需联系二阶导数图形)。
分步拆解:将复杂问题分解为多个子问题。例如,求解含参数的微分方程时,先分离变量再讨论参数范围。
特值验证:选择题中代入特殊值(如x=0或1)可快速排除错误选项。2025年数学三第8题通过特值法节省了70%的解题时间。
图形辅助:几何问题绘制草图可直观分析极值点或积分区域,避免抽象思维误差。
3. 错题管理:精准突破薄弱点
建立分类错题本(如“计算错误”“概念混淆”),定期统计高频错误类型。
对同一类错题进行变式训练。例如,若二重积分区域判断错误,可练习5道不同坐标系的同类题目。
四、备考策略:科学规划与资源利用
1. 三阶段复习法
基础期(3-6个月):以教材(如同济版《高等数学》)为核心,完成1800题基础篇,重点理解定理推导过程。
强化期(2-3个月):精研真题(2015-2025年),按模块分类练习,并总结命题规律。
冲刺期(1个月):全真模拟考试,控制答题时间(选择题每题≤5分钟),训练心理素质。
2. 资源推荐
教辅资料:张宇《真题大全解》、李永乐《线性代数辅导讲义》覆盖90%以上考点。
课程选择:汤家凤基础班适合零基础考生,李永乐强化班侧重解题技巧。
考研数学的突破不仅依赖大量练习,更需要系统性的分析与策略调整。通过高频考点的精准把握、真题规律的深度挖掘及科学解题技巧的应用,考生可显著提升备考效率。正如2024年数学高分考生反馈:“每道错题都是进步的阶梯,每次真题训练都是思维的淬炼。”坚持科学方法,必能在考场上游刃有余。