WHUT编译原理真题解析-核心考点与典型例题剖析

编译原理作为计算机科学的核心课程，是理解程序运行机制和语言设计的关键，其理论性与实践性并重的特点使得学生在备考时既需掌握抽象概念，又需熟练应用解题技巧。本文基于武汉理工大学编译原理课程的历年真题与教学大纲，剖析高频考点与典型题型，为考生提供系统化的复习策略与解题思路。

一、核心考点解析

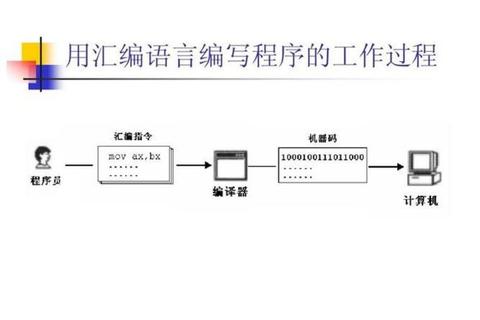
编译原理的知识体系可分为文法与语言分析、词法与语法处理、中间代码生成与优化三大模块。以下结合真题案例，总结各模块的核心内容：

1. 文法与语言分析

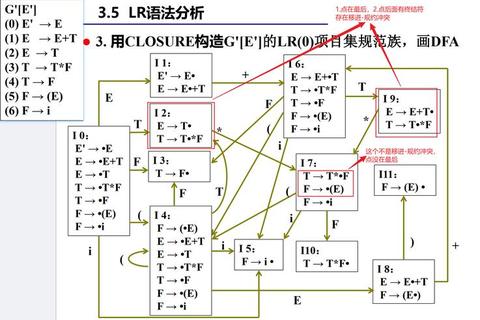
考点重点：文法的分类（0-3型文法）、推导方法（最左/最右推导）、句型与句子的区别、二义性证明。

真题示例：

> 给定文法G：S → aSb | ε，判断其生成的语言类型，并写出字符串“aaabbb”的最左推导过程。

解析：

该文法属于2型文法（上下文无关文法），其语言为{a^n b^n | n≥0}。最左推导过程为：

S ⇒ aSb ⇒ aaSbb ⇒ aaaSbbb ⇒ aaabbb（推导三次后展开ε）。

备考提示：需熟练掌握如何通过文法规则构造推导树，并理解不同文法类型对语言能力的差异。

2. 词法与语法分析

考点重点：正则表达式与有限自动机（NFA/DFA）的转换、LL(1)文法判定、LR分析表的构造。

真题示例：

> 将正则表达式(a|b)abb转换为等价NFA，并进一步确定化为DFA。

解析：

通过Thompson算法构建NFA后，利用子集构造法消除ε边，最终得到最小化的DFA状态转移表。

备考提示：需掌握FIRST集与FOLLOW集的计算方法，以及如何通过预测分析表解决LL(1)冲突。

3. 中间代码生成与优化

考点重点：语法制导翻译、三地址代码生成、循环优化技术（如强度削弱、代码外提）。

真题示例：

> 将表达式a(b+c)转换为逆波兰表示，并生成对应的四元式序列。

解析：

逆波兰式为“abc+”，对应的四元式为：

(+, b, c, T1)

(, a, T1, T2)

备考提示：需熟悉不同中间代码形式（如后缀式、DAG图）的生成规则，并理解局部优化与全局优化的区别。

二、典型例题剖析

以下从近年真题中选取代表性题型，分类解析解题思路：

1. 文法推导与归约题

题型特点：要求根据文法规则构造推导过程或识别句柄。

例题：消除文法S→Sa|b的直接左递归。

解析：

改写为S→bS'，S'→aS'|ε。通过引入新非终结符消除左递归，确保语法分析器的确定性。

2. 语法树与二义性证明题

题型特点：需构建同一句子的两棵不同语法树以证明文法二义性。

例题：证明文法E→E+E|EE|id存在二义性。

解析：

对表达式“id+idid”，可分别以“加法优先”或“乘法优先”构造语法树，表明文法未定义运算符优先级。

3. 代码优化应用题

题型特点：要求对中间代码进行优化，如删除公共子表达式或冗余赋值。

例题：优化以下代码：

T1 = a + b

T2 = T1 c

T3 = a + b

解析：

识别T1与T3为公共子表达式，合并后代码简化为：

T1 = a + b

T2 = T1 c。

三、备考策略与资源推荐

1. 分阶段复习法

基础阶段：梳理核心概念（如属性文法的综合属性与继承属性），结合课本例题巩固推导与归约技巧。

强化阶段：通过八套真题模拟训练（推荐资源库“编译原理期末试题(八套含答案+大题集)”），重点突破语法分析与代码优化难题。

冲刺阶段：利用错题本总结高频易错点（如LR分析表构造中的移进-归约冲突），模拟考试环境限时答题。

2. 工具与资源推荐

在线课程：中国大学MOOC平台“编译原理”课程提供完整的语法树构建与中间代码生成演示。

习题库：参考《编译原理期末复习及真题详解》中的选择题与判断题，快速检验知识盲区。

实践工具：使用Flex与Bison工具链实现简易编译器，深化对词法/语法分析器的理解。

四、

编译原理的学习不仅是应对考试的必要准备，更是培养计算思维与工程能力的重要途径。通过系统化的考点梳理、真题解析与策略规划，考生可显著提升解题效率与应试信心。最终目标并非仅追求高分，而是真正掌握“从源代码到可执行程序”的全链条逻辑，为未来从事编译器开发或语言设计奠定坚实基础。