反常积分的计算与判敛是考研数学的核心考点之一,其题型灵活多变,对考生的综合分析与计算能力要求较高。本文结合近十年考研数学(二)真题,系统梳理反常积分的核心方法、典型例题解题思路及备考策略,帮生突破这一难点。
一、反常积分的基本概念与核心方法
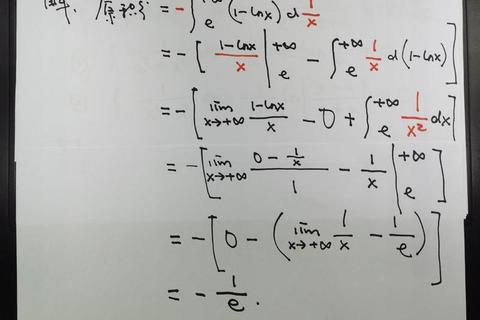
反常积分分为无穷区间积分与瑕积分两类,其核心在于通过极限思想处理积分区间的无限性或被积函数的性。根据考研大纲要求,考生需掌握以下四大核心方法:
1. 定义法(直接计算法)
当被积函数的原函数易于求解时,直接计算积分极限。例如,计算 (int_{1}^{+infty} frac{1}{x^p} dx),其结果为 (lim_{b
o +infty} int_{1}^{b} frac{1}{x^p} dx)。当 (p>1) 时收敛,(p leq 1) 时发散。
适用场景:原函数易求或可通过变量替换简化(如含 (e^x) 或三角函数的情形)。
2. 比较判别法
通过与被积函数的主部(如 (1/x^p))比较,判断敛散性。例如,判断 (int_{1}^{+infty} frac{1}{sqrt{x^3+1}} dx) 的收敛性时,因 (frac{1}{sqrt{x^3+1}} leq frac{1}{x^{3/2}}),而后者积分收敛,故原积分收敛。
关键原则:
3. 区间拆分法
针对同时含无穷区间和瑕点的混合型积分,需拆分为独立的无穷积分与瑕积分分别判断。例如,(int_{0}^{+infty} frac{1}{x^2 sqrt{x-1}} dx) 需拆分为 (int_{0}^{1} frac{1}{x^2 sqrt{x-1}} dx)(瑕点 (x=1))与 (int_{1}^{+infty} frac{1}{x^2 sqrt{x-1}} dx)(无穷区间),分别计算其收敛性。
4. 振荡函数处理法
对含 (sin x)、(cos x) 等振荡项的积分,使用 Dirichlet判别法 或 Abel判别法。例如,(int_{1}^{+infty} frac{sin x}{x^p} dx) 在 (p>0) 时收敛,因振荡项积分有界,且 (1/x^p) 单调趋于零。
二、典型真题解析与解题技巧

例题1(2022年数学二第5题)
计算 (int_{2}^{+infty} frac{1}{(x+7)sqrt{x-2}} dx)。
解析:
1. 类型识别:无穷区间积分。
2. 变量替换:令 (t = sqrt{x-2}),则 (x = t^2 + 2),积分转化为 (int_{0}^{+infty} frac{2t}{(t^2+9)t} dt = 2 int_{0}^{+infty} frac{1}{t^2+9} dt)。
3. 计算结果:利用公式 (int frac{1}{t^2+a^2} dt = frac{1}{a} arctan frac{t}{a}),结果为 (frac{pi}{3})。
例题2(2010年数学二第21题)
讨论 (int_{1}^{+infty} frac{ln x}{x^p} dx) 的收敛性。
解析:
1. 主部分析:当 (x
o +infty),(ln x) 增长速度远低于幂函数,故被积函数主部为 (1/x^p)。
2. 比较判别:因 (frac{ln x}{x^p} leq frac{1}{x^{p-epsilon}})((epsilon) 为任意小正数),当 (p-epsilon >1) 即 (p>1) 时积分收敛。
3. 结论:积分在 (p>1) 时收敛,(p leq 1) 时发散。
例题3(混合型积分)
判断 (int_{0}^{+infty} frac{1}{x^a (1+x)^b} dx) 的收敛性。
解析:
1. 拆分区间:分为 (int_{0}^{1} frac{1}{x^a (1+x)^b} dx) 和 (int_{1}^{+infty} frac{1}{x^a (1+x)^b} dx)。
2. 局部分析:
3. 综合结论:当 (a<1) 且 (a+b>1) 时积分收敛。
三、易错点与备考策略
易错点警示
1. 忽略隐藏瑕点:如 (int_{-1}^{1} frac{1}{x^2} dx) 在 (x=0) 处存在瑕点,需拆分为两段计算。
2. 参数讨论不全:含参数的积分需分段讨论临界值(如 (p=1) 或 (p=2))。
3. 误用对称性:奇函数在对称区间积分收敛的前提是积分本身收敛,不可直接判定为零。
备考策略
1. 分阶段强化:
2. 真题精练:近十年真题中,反常积分平均每年考查1-2题,建议逐题分析解题步骤,提炼核心方法。
3. 公式记忆:考前重点记忆 (p) 积分与 (q) 积分的收敛条件:
反常积分的解题能力是考研数学高分的关键之一。考生需从定义出发,结合比较、拆分、振荡处理等技巧,逐步构建系统化的解题框架。通过真题演练与易错点总结,可显著提升对复杂题目的应对能力。最终目标不仅是掌握方法,更是形成快速识别题型、精准选择工具的思维习惯,从而在考场上游刃有余。


