二重积分作为考研数学中的重要考点，其掌握程度直接关系到考生在高等数学部分的得分能力。 这一题型不仅考查学生对多元函数积分理论的理解，更强调对几何直观、计算能力以及解题策略的综合运用。本文将从二重积分的核心题型出发，结合近年考研真题，系统剖析解题技巧，并提供科学的备考建议，助力考生突破这一难点。

一、二重积分在考研数学中的定位与考查特点

考研二重积分真题解析_核心题型与解题技巧深度剖析

二重积分是多元函数积分学的核心内容，其重要性体现在三个方面：一是作为后续三重积分、曲线积分的基础；二是与物理应用（如质心、转动惯量）紧密相关；三是命题形式灵活，常与其他章节（如微分方程、级数）结合考查。通过对近十年考研真题的统计分析，二重积分在数学一、数学二、数学三试卷中的分值占比均超过5%，且题型覆盖计算题、证明题和应用题。

命题趋势表明，二重积分题目的难点逐渐从单纯的计算转向对“积分区域分析”和“积分次序选择”的考查。例如，2023年数学一真题中，一道关于极坐标下分段积分的问题，要求考生先通过对称性化简区域，再结合分段讨论完成计算，充分体现了对综合能力的考核。

二、二重积分的基本题型分类与解题思路

考研二重积分真题解析_核心题型与解题技巧深度剖析

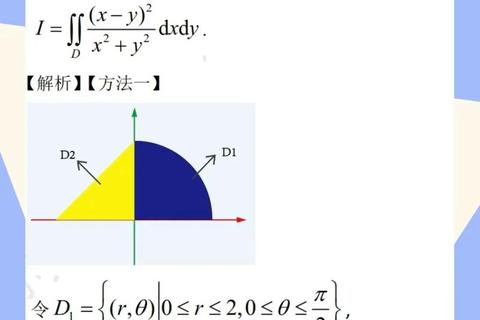
1. 基础计算型：直角坐标系与极坐标系的转换

核心技巧：

  • 区域划分法：当积分区域由直线或简单曲线围成时，优先选择直角坐标系。例如，区域D由( y=x )、( y=2x )和( x=1 )组成时，可通过确定x和y的上下限直接计算。
  • 极坐标转换条件：若积分区域为圆、扇形或环形（如( x^2 + y^2 leq R^2 )），或被积函数含( x^2 + y^2 )，则优先使用极坐标系。转换时需注意雅可比行列式（即增加r因子）。

    • 真题示例（改编自2021年数学二真题）：

    计算( iint_D (x^2 + y^2) , dxdy )，其中D为由( x^2 + y^2 = 2x )围成的区域。

    解析：将方程( x^2 + y^2 = 2x )化为极坐标形式( r = 2cos

    heta )，积分区域对应θ范围( [-pi/2, pi/2] )，r范围( [0, 2cos

    heta] )。最终积分转换为( int_{-pi/2}^{pi/2} int_0^{2cos

    heta} r^3 , dr d

    heta )，计算后得结果( 3pi )。

    2. 对称性应用型：简化计算的利器

    核心技巧：

  • 奇偶对称性：若区域D关于x轴对称，且被积函数关于y为奇函数，则积分值为0；若为偶函数，可计算一半区域后加倍。
  • 轮换对称性：当区域D关于( y=x )对称时，( iint_D f(x,y) , dxdy = iint_D f(y,x) , dxdy )，可用于化简复杂表达式。

    • 典型错误：忽略对称性条件直接化简，例如将非对称区域误判为对称区域，导致结果错误。

    3. 分段积分型：复杂区域的分解策略

    核心技巧：当积分区域由不同表达式定义（如分段函数边界）时，需将区域划分为若干子区域，分别积分后求和。例如，2020年数学三真题中，区域D由( y=x^2 )和( y=1 )围成，需拆分为左右两部分计算。

    三、典型错误分析与规避策略

    1. 积分次序选择不当

    案例：计算( iint_D frac{sin y}{y} , dxdy )，其中D由( y=x )、( y=sqrt{x} )围成。若先对y积分，需处理( int frac{sin y}{y} , dy )，无法用初等函数表示；正确方法应为先对x积分，转化为( int_0^1 int_{y^2}^y frac{sin y}{y} , dx dy )，简化后得到( int_0^1 sin y (1

  • y) , dy )。

    • 规避策略：选择积分次序时，优先考虑被积函数的特点。若先积分的变量无法求出原函数，则需调整次序。

    2. 极坐标转换遗漏细节

    常见错误：忽略θ的范围（如将圆形区域的θ误设为( [0, 2pi] )而未考虑实际图形），或忘记添加r因子。

    规避策略：绘制区域图形，明确θ和r的上下限；转换后检查积分表达式是否包含r。

    四、备考策略与实战建议

    1. 分阶段训练法

  • 基础阶段：掌握直角坐标与极坐标的积分方法，熟记对称性、奇偶性等性质。推荐使用《同济高等数学》教材配套习题。
  • 强化阶段：重点突破分段积分、参数方程区域等复杂题型，结合《李永乐复习全书》中的综合例题进行专项训练。
  • 冲刺阶段：通过历年真题限时模拟，分析错题原因，总结高频考点（如极坐标转换、对称性应用）。

    • 2. 时间分配与计算准确性

  • 时间建议：考场上解答一道二重积分题应控制在15分钟内，其中5分钟分析区域与选择方法，10分钟完成计算。
  • 准确性提升：采用“逆向验证法”，即通过交换积分次序或改变坐标系重新计算，对比结果是否一致。

    • 五、

    二重积分的突破关键在于“区域分析优先，方法选择灵活，计算过程严谨”。考生需通过系统训练，将解题步骤内化为条件反射，同时注重细节规避常见错误。在备考中，建议结合真题反复演练，并利用错题本记录易错点，最终实现从“会做”到“快且准”的跨越。唯有将理论理解与实战技巧深度融合，方能在考场上游刃有余，稳操胜券。