区间估计作为统计学中的重要分支,在考研数学中占据关键地位,尤其在参数估计与假设检验部分常以压轴题形式出现。其核心在于通过样本数据推断总体参数的置信范围,既考察考生对概率论基础知识的掌握,又检验逻辑推理与计算能力。本文将结合考研真题特点,系统解析区间估计的核心考点、解题技巧及备考策略,助力考生突破这一难点。
一、区间估计的核心考点解析
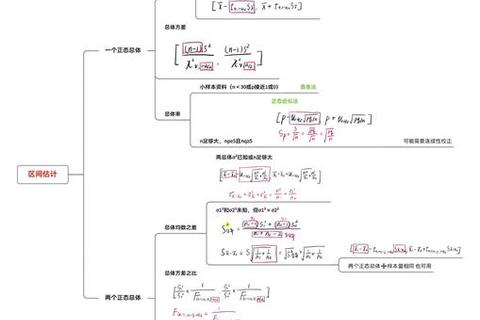
区间估计的核心逻辑围绕置信水平、枢轴量构造和分布选择展开,需重点掌握以下三类情境:
1. 单正态总体均值区间估计
2. 双正态总体均值差的区间估计
当两个总体独立且方差未知但相等时,构造合并方差 $s_p^2 = frac{(n_1-1)s_1^2 + (n_2-1)s_2^2}{n_1+n_2-2}$,置信区间为 $(bar{X}_1
3. 非正态总体的近似处理
当总体分布未知但样本量较大(n≥30)时,利用中心极限定理近似为正态分布。例如,某真题中通过指数分布样本构造枢轴量 $T=frac{2sum |X_i|}{
heta} sim chi^2(2n)$,进而推导θ的置信区间。
二、考研真题常见题型与解题技巧
从近十年真题来看,区间估计的考查形式集中在以下三类题型:
1. 基础计算题
特征:直接套用公式,但需注意条件判断。
示例:已知某城市通勤时间样本均值 $bar{X}=120$分钟,标准差 $s=30$,样本量 $n=100$,求总体均值95%的置信区间。
解法:因n=100(大样本),使用Z分布,区间为 $120 pm 1.96
imes frac{30}{sqrt{100}} = [114.12, 125.88]$。
易错点:误用t分布或忽略样本标准差与总体标准差的区别。
2. 综合应用题
特征:结合分布性质或参数转换,需多步骤推导。
示例:若总体 $X sim N(mu, sigma^2)$,已知$frac{u_{0.025}}{u_{0.05}}=k$,求从90%置信区间 $(a,b)$ 推导95%置信区间。
关键技巧:
3. 非参数化问题
特征:总体分布非正态或参数复杂,需构造特殊枢轴量。
示例:对于密度函数 $f(x;
heta)=frac{1}{2
heta}e^{-|x|/
heta}$,利用 $T=sum |X_i|$ 且 $frac{2T}{
heta} sim chi^2(2n)$ 的性质,求θ的置信区间。
突破点:识别统计量的分布类型,将问题转化为卡方分布或F分布的分位数计算。
三、解题策略与常见误区
1. 分步拆解法
2. 代数转换技巧
当题目涉及置信水平变化时(如从90%提升至95%),可通过临界值比例关系反向推导。例如,已知 $u_{0.05}=1.645$,若要求新区间宽度不变但置信水平提高,需调整样本量 $n$。
3. 易错点警示
四、备考建议与资源利用
1. 夯实基础理论
重点复习三大分布(Z、t、卡方)的性质及适用条件,熟记单双总体区间估计公式。推荐通过思维导图梳理知识框架(如图1)。
2. 强化真题训练
近十年真题中,区间估计大题常与假设检验结合。建议专项练习2015年、2018年、2021年真题,分析命题趋势。
3. 提升计算效率
熟练使用分位数表(如 $z_{0.025}=1.96$,$t_{0.025}(10)=2.228$),避免考试中因查表耽误时间。推荐制作常用临界值速记卡。
4. 模拟实战演练
针对压轴题特点,进行限时训练(建议25分钟内完成一道综合题),培养快速识别条件与选择方法的能力。
区间估计作为连接概率论与统计应用的桥梁,其掌握程度直接影响考研数学高分突破。考生需从理论理解、题型归纳、计算强化三方面入手,结合真题反复打磨解题逻辑。尤其需注意,近年考题逐渐偏向综合化与创新性(如非正态分布与多参数估计),唯有深入理解原理,方能以不变应万变。


