在考研这场智力与耐力的双重考验中,数学作为决定性科目,其真题的合理规划与高效运用是突破高分的关键。本文从时间管理、策略优化与重难点突破三个维度,结合教育学理论与实战经验,为考生构建一套科学、可落地的复习框架,助力实现“真题价值最大化”。
一、真题的核心价值:从认知到应用的三重维度
真题不仅是检验知识水平的工具,更是命题逻辑的镜像。近十年真题中,80%的题目围绕基础知识点展开,如极限、导数、积分等核心概念。通过系统分析可发现两大规律:
1. 题型稳定性:如中值定理证明题每年必考,且解题思路高度依赖构造函数与定理联动的模板;
2. 陷阱共性:分段函数连续性、变限积分求导等知识点常通过“定义域突变”“符号错误”等细节设置干扰项。
考生需将真题视为“动态数据库”,通过纵向对比(如2018与2023年级数题型演变)提炼出题趋势,横向归纳高频考点与解题范式,从而将被动刷题转化为主动预判。
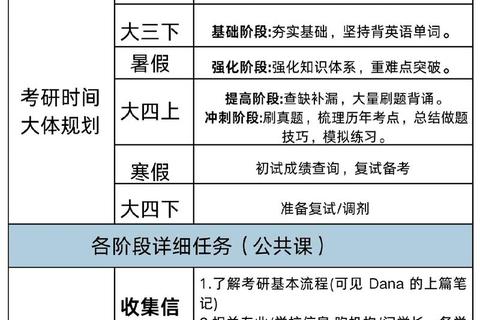
二、时间规划:三阶递进模型实现质变
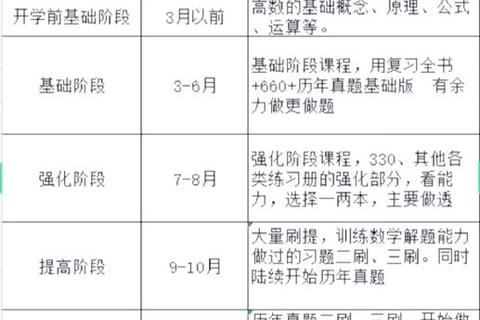
基于艾宾浩斯记忆曲线与刻意练习理论,建议将真题训练划分为三个阶段:
1. 基础巩固期(8月前)——构建知识网络
任务目标:完成近15年真题分类练习,建立知识点与题型的映射关系。
执行策略:
按章节拆分真题(如将所有极限题集中训练),标注每道题的考点及易错点(如洛必达法则的适用条件);
搭配《复习全书·基础篇》进行概念溯源,针对错误率>40%的题型回归教材推导(如泰勒公式展开原理);
每日完成30题+1小时错题复盘,形成“问题发现-理论强化-二次练习”闭环。
2. 专项突破期(9-10月)——攻克能力盲区
任务目标:针对薄弱模块(如微分方程建模、级数敛散性判断)进行定向突破。
执行策略:
利用错题本筛选顽固题型,采用“10题连刷法”集中训练(如连续完成10道矩阵相似判定题);
引入《660题》等教辅进行变式拓展,掌握“一题多解”技巧(如参数方程与直角坐标的双路径积分计算);
每周进行一次限时模考(2.5小时/套),逐步压缩选择题耗时至50分钟内。
3. 全真模拟期(11-12月)——提升应试韧性
任务目标:通过套卷训练优化时间分配与心态调节能力。
执行策略:
严格模拟考场环境(上午8:30-11:30),按“选择60分钟→填空20分钟→解答70分钟”分配时间;
分析每套卷的得分结构(如证明题得分率低于50%需强化定理推导);
使用《张宇8套卷》等高难度模拟题进行抗压训练,培养“跳跃解题”意识(暂时搁置卡壳题,优先确保基础分)。
三、高效策略:四维方法论激活真题潜力
1. 三轮刷题法——深度挖掘题目价值
首轮:关注解题正确率与知识点覆盖,用红笔标注思路卡点;
二轮:聚焦错题,分析错误类型(知识盲区用红色、思维漏洞用蓝色、计算失误用黑色);
三轮:横向对比同类题,总结命题规律(如几何应用常考旋转体体积与曲面积分的组合考查)。
2. 错题本动态管理——践行“减法思维”
每月移除已掌握题目,仅保留反复出错的“钉子户”;
对典型错题附加“考点溯源标签”(如标注“2022真题→极坐标积分区域画法错误”)。
3. 命题人视角训练——逆向拆解真题
对高正确率题目(>90%)进行“反向出题”:保留题干条件,自主设计干扰选项;
对比真题与模拟题的设问差异(如真题常通过“隐式条件”增加难度,而模拟题倾向复杂计算)。
4. 公式场景化记忆——突破记忆瓶颈
将易混公式(如格林公式、高斯公式)与真题例题绑定记忆(如联想2021年某题对应的高斯公式应用场景);
在书桌张贴“高频公式思维导图”,利用碎片时间进行视觉强化。
四、重难点突破:三类题型的针对性解决方案
1. 证明题:逻辑链构建法
中值定理类:按照“条件提取→定理匹配→辅助函数构造→验证完备性”四步解题;
不等式类:优先考虑泰勒展开或单调性分析,例如利用$f''(x)>0$证明凸函数性质。
2. 综合应用题:数学语言转译法
将物理问题(如变力做功)转化为定积分表达式时,注意单位统一与积分上下限的物理意义;
经济类问题(如边际成本计算)需区分导数与积分的经济学解释差异。
3. 计算题:分步校验法
二重积分计算遵循“画区域→选坐标系→定次序→分部积分”流程,每步完成后逆向验证;
矩阵运算采用“行列式+迹”双重检验,避免特征值计算错误。
五、从量变到质变的科学路径
考研数学的高分突破,本质是通过真题的精细化运营,将零散知识点转化为系统解题能力的过程。考生需摒弃“题海战术”的盲目性,转而建立“分析-迭代-验证”的科学循环。当每一道真题的价值被充分激活时,考场上的从容应对便成为水到渠成的必然。
> 特别提示:本文方法论需配合《考研数学真题真刷》《复习全书·基础篇》等资料使用,具体进度可根据个人基础调整,但需确保三个阶段的有效衔接。唯有坚持“真题为纲、反思为镜、策略为器”,方能在数学战场上实现从“跟跑”到“领跑”的跨越。
参考文献:




