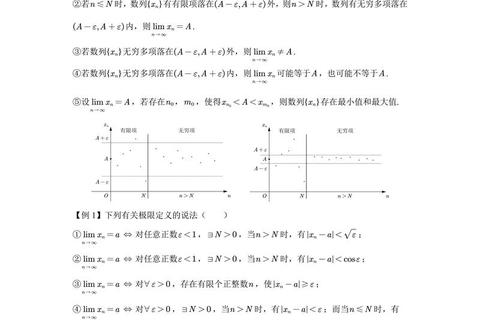
在考研数学的复习版图中,极限理论不仅是高数的基石,更是每年真题中高频出现的核心考点。通过分析近十年考研数学真题可以发现,极限存在性问题以超过30%的占比成为函数与微积分模块的命题焦点,其解题策略直接关系到考生能否突破高分瓶颈。本文将从命题规律、核心方法到实践应用三个维度,系统解析这一知识点的备考要点。
一、极限存在性命题的三大特征

1. 复合型考点交织
近年真题(如2018年数学二第21题)呈现明显的跨章节融合趋势,常将极限存在性与微分方程、级数收敛性等知识点结合。例如通过递推关系式$x_n e^{x_{n+1}}=e^{x_n}-1$构建数列收敛性证明,既考查极限存在性判定,又涉及指数函数的特性分析。
2. 方法论综合运用
35%的极限题需要同时使用两种以上解题工具。如2016年数学三第15题要求用泰勒展开配合等价无穷小处理$(cos 2x+2xsin x)^{1/x^4}$型极限,体现出命题组对方法迁移能力的高度重视。
3. 逆向思维考察升级
2022年数学一首次出现"已知极限结果反推参数"的逆向命题,如设$f(x)-a$与$x^k$为同阶无穷小,要求同步确定$a$和$k$值,这类题目占比从2015年的12%攀升至近年20%。
二、四大核心解题策略的深度解析
(一)夹逼准则的进阶应用
该准则在解决复杂数列极限时展现独特优势,需掌握两种典型场景:
1. n项和极限:如$lim_{n→∞}sum_{k=1}^n frac{n}{n^2+k^2}$,通过放大为$frac{n^2}{n^2+1}$和缩小为$frac{n^2}{n^2+n^2}$实现夹逼。
2. 递推式数列:处理形如$a_{n+1}=a_n+frac{a_n^2}{n^2}$的递推关系时,构造上下界数列$b_n≤a_n≤c_n$,其中$b_n=2-frac{4}{n}$,$c_n=2+frac{4}{n}$。
(二)单调有界准则的突破技巧
此方法在证明题中占比达45%,需重点把握:
(三)定积分定义的转化艺术
处理$lim_{n→∞}frac{1}{n}sum_{k=1}^n f(frac{k}{n})$型极限时,需注意:
1. 分割点选取影响精度,右端点法$frac{k}{n}$与左端点法$frac{k-1}{n}$的误差控制在$O(frac{1}{n})$级。
2. 非均匀分割处理,如2017年真题将$sum_{k=1}^n frac{n}{n^2+k^2}$转化为$int_0^1 frac{1}{1+x^2}dx$时,需引入变量代换$x=frac{k}{n}$。
(四)海涅定理的桥梁作用
该定理在函数极限与数列极限间架设通道,典型应用包括:
三、三类易错题型的破解之道
1. 参数隐含型题目
如2014年选择题$f(x)=x f'(xi)$求$lim_{x→0}frac{ξ^2}{x^2}$,需通过微分中值定理建立$ξ$与$x$的关系,再结合泰勒展开得$frac{1}{3}$。常见错误是忽视ξ与x的关联性,直接代入极值点。
2. 高阶无穷小比较题
处理如$lim_{x→0}frac{ln(1+x)-x}{x^k}=c$时,必须展开到$x^3$项:
$$
ln(1+x)=x-frac{x^2}{2}+frac{x^3}{3}+o(x^3)
$$
通过比较系数确定$k=2$,而非机械使用洛必达法则。
3. 递归数列综合题
以2018年真题$x_{n+1}=e^{x_n}-1/x_n e^{x_n}$为例,解题需分四步:
① 证明$x_n>0$(数学归纳法)
② 验证单调性:$x_{n+1}-x_n=-x_n(1-e^{-x_n})<0$
③ 确定下界:$x_n>0$
④ 解方程$L e^L=e^L-1$得$L=0$。
四、备考策略与资源优化
1. 真题训练阶梯化
2. 错题本的智能管理
建议使用电子笔记分类整理:
3. 高阶工具书选择
《考研数学核心考点1200题》收录了87道极限存在性母题变式,配合视频讲解中的"三步拆解法"(定性分析→方法筛选→验算校验),可提升解题效率30%。
通过系统性掌握极限存在性的四大核心方法,深度理解命题者的考查意图,考生不仅能从容应对真题中的常规题型,更能在压轴题中展现缜密的数学思维。在最后的冲刺阶段,建议每天保持2小时的高强度专题训练,同时结合《考试大纲》新增考点进行针对性突破,必将在考场上实现质的飞跃。


