心理学考研中,心理统计学因其抽象性和应用性成为考生备考的难点之一。通过系统分析历年真题,可以发现高频考点与重点题型具有显著规律性,掌握这些规律不仅能提升复习效率,还能帮生在考试中精准定位得分点。本文从知识框架、核心题型、解题策略三个维度展开剖析,结合备考建议,为考生提供实用指南。
一、高频考点聚焦:统计学的“四梁八柱”
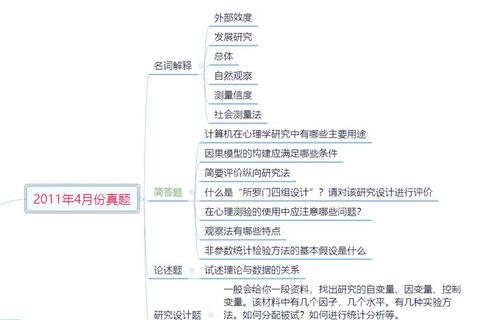
心理统计学的核心考点集中于推断统计,占比超过70%。具体表现为以下五大模块:
1. 假设检验与参数估计
核心要点:两类错误(α错误与β错误)的辨析、单侧与双侧检验的适用条件、置信区间的计算。例如,2022年真题要求判断“某城市三种神经症患者比例是否变化”,需通过卡方检验完成假设检验。
解题关键:区分总体方差已知(Z检验)与未知(t检验)的条件,熟练运用公式(如$bar{X} pm Z_{alpha/2} frac{sigma}{sqrt{n}}$)。
2. 方差分析(ANOVA)
考查形式:多因素方差分析的交互作用判定、事后检验方法(如法)。如2013年真题中,通过方差分析表补全自由度与均方值,需掌握组内变异与组间变异的计算逻辑。
易错点:忽略方差齐性检验(如Levene检验)的前提条件,导致误用F检验。
3. 相关与回归分析
重点题型:积差相关与等级相关的选择(如连续变量用Pearson,顺序变量用Spearman)、回归方程的推导。2014年真题要求根据动机水平与成绩的相关系数(r=0.95)计算决定系数($r^2=0.9025$),并建立回归方程。
拓展应用:区分相关关系与因果关系的逻辑差异,避免混淆。
4. 非参数检验
典型例题:卡方拟合优度检验(如2016年神经症比例变化检验)及独立性检验(如2011年性别与游戏选择差异分析)。
特殊场景:当数据不符合正态分布或样本量较小时,需优先选择卡方检验、曼-惠特尼U检验等非参数方法。
二、重点题型解析:从公式到实战

心理统计真题可分为计算题、概念题和综合应用题三类,其解题逻辑各有侧重:
1. 计算题:公式的精准运用
高频公式:标准差($sigma=sqrt{frac{sum(X-bar{X})^2}{N}}$)、t值($t=frac{bar{X}-mu}{s/sqrt{n}}$)、卡方值($chi^2=sumfrac{(O-E)^2}{E}$)。例如,2017年真题要求计算测验分数的正态性检验,需结合频数分布表进行卡方拟合检验。
技巧提示:单位换算与符号保留(如保留两位小数),避免因计算失误失分。
2. 概念题:理论的理解与对比
典型问题:正态分布与标准正态分布的区别(均值与标准差不同)、参数估计与假设检验的关系(前者用样本推断总体参数,后者验证假设)。如2008年真题直接考查两者的异同。
记忆策略:通过思维导图对比相似概念(如中位数、众数、均值的优缺点),强化理解。
3. 综合应用题:实验设计与统计的结合
常见场景:实验设计的方差分析(如随机区组设计、重复测量设计)、数据结果解读。2022年真题要求根据方差分析表判断实验设计类型,并解释主效应与交互作用。
答题框架:先明确实验变量(自变量与因变量),再选择统计方法,最后结合P值得出结论。
三、备考策略:科学规划与高效突破
1. 分阶段复习法
基础阶段:以张厚粲《现代心理与教育统计学》为核心,重点掌握统计(如集中量数、差异量数)与推断统计基础(如Z分布、t分布)。
强化阶段:通过真题分类训练(如近10年假设检验真题汇总),总结高频错误类型(如忽略方差齐性检验)。
冲刺阶段:模拟考试环境,限时完成综合题型(如2018年问卷信效度分析与差异检验结合题),提升应试速度。
2. 错题管理与专项突破
建立错题本:记录公式误用(如混淆样本方差与总体方差)、概念混淆(如Ⅰ类错误与Ⅱ类错误的实际意义)等问题,定期复盘。
专项训练:针对薄弱环节(如回归分析)进行专题突破,参考《心理统计学考研题库》中的典型题解析。
3. 工具与资源利用
统计软件辅助:使用SPSS或Excel验证计算结果(如方差分析表),直观理解输出结果的含义。
教辅资料推荐:结合《心理统计与测量基础阶段复习指南》梳理知识框架,利用《阿范题:刷题宝典》强化实战能力。
四、
心理统计学的备考需以真题为导向,紧扣高频考点(如假设检验、方差分析)与重点题型(如综合应用题),通过系统训练与策略优化,将抽象公式转化为解题工具。考生需注重知识体系的完整性(如区分参数与非参数检验),同时强化实战能力(如限时模拟),方能在考场上游刃有余。最终,统计学不仅是考试科目,更是未来科研与实践中分析数据、验证假设的重要思维工具,其价值远超分数本身。




