2014年数学三考研真题解析_高频考点与解题思路深度剖析

在考研数学三的备考过程中，真题的深度解析与高频考点的梳理是提升应试能力的关键。2014年数学三试题不仅体现了基础性与综合性的结合，更通过典型题目揭示了核心考点的命题规律。本文将从高频考点分布、典型题目解析、解题思路提炼及备考策略四个维度展开分析，帮生构建系统性复习框架。

一、高频考点分布与命题特点

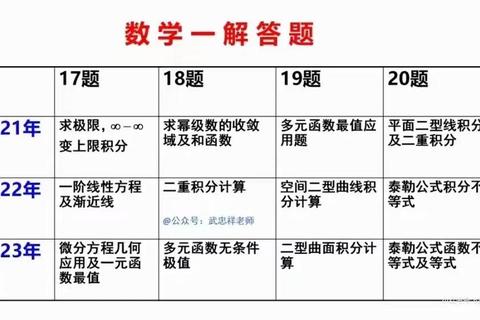
2014年数学三试题的考点分布延续了往年的核心框架，以高等数学、线性代数、概率论与数理统计三大板块为主体。通过对真题的拆解，高频考点可归纳如下：

1. 高等数学（占比约56%）：

极限与连续：考查分段函数极限、连续性判断及间断点分类（如选择题第1题）。

一元函数微分学：隐函数求导、极值问题及微分中值定理的应用（如解答题第17题）。

积分学：定积分计算、变上限积分求导及积分中值定理（如填空题第9题）。

多元函数微分学：偏导数与全微分的计算、条件极值的求解（如解答题第18题）。

2. 线性代数（占比约22%）：

矩阵与行列式：矩阵运算、行列式性质及分块矩阵的应用（如选择题第5题）。

线性方程组：解的判定、齐次与非齐次方程组的通解结构（如解答题第20题）。

二次型：标准化方法、特征值与特征向量的应用（如解答题第21题）。

3. 概率论与数理统计（占比约22%）：

随机变量分布：离散型与连续型变量的分布函数及期望计算（如解答题第22题）。

统计量性质：样本均值与方差的分布、参数估计方法（如解答题第23题）。

命题特点：试题强调基础概念的灵活运用，例如通过矩阵方程考查线性方程组的转化能力（如解答题第20题），以及利用积分对称性简化计算（如填空题第9题）。题目设计中常隐含跨章节知识的综合应用，例如将微分方程与积分结合考查。

二、典型题目解析与思路拆解

1. 高等数学典型题：变上限积分与极限结合（填空题第9题）

题目：计算极限 ( lim_{x

o +infty} x^2 left( e^{frac{1}{x}}

1

frac{1}{x} right) )。

解析：

步骤1：利用泰勒展开简化表达式。将 ( e^{frac{1}{x}} ) 展开至二阶：

[

e^{frac{1}{x}} = 1 + frac{1}{x} + frac{1}{2x^2} + oleft( frac{1}{x^2} right)

]

步骤2：代入原式并化简：

[

x^2 left( frac{1}{2x^2} + oleft( frac{1}{x^2} right) right) = frac{1}{2} + o(1)

]

结论：极限值为 ( frac{1}{2} )。

关键点：泰勒展开的应用是解决高阶无穷小问题的核心技巧。

2. 线性代数典型题：矩阵方程与线性方程组（解答题第20题）

题目：设矩阵方程 ( AX + B = X )，求未知矩阵 ( X )。

解析：

步骤1：将方程改写为 ( (A

I)X = -B )，其中 ( I ) 为单位矩阵。

步骤2：判断系数矩阵 ( A

I ) 是否可逆。若可逆，则 ( X = -(A - I)^{-1}B )；若不可逆，需通过初等行变换求解通解。

关键点：矩阵方程的求解依赖于矩阵运算性质及逆矩阵的存在性判断。

3. 概率论典型题：随机变量函数的分布（解答题第22题）

题目：设 ( X sim U(0,1) )，求 ( Y = -ln X ) 的概率密度函数。

解析：

步骤1：确定 ( Y ) 的取值范围为 ( (0, +infty) )。

步骤2：利用分布函数法，计算 ( P(Y leq y) = P(-ln X leq y) = P(X geq e^{-y}) )。

步骤3：求导得密度函数 ( f_Y(y) = e^{-y} )（( y > 0 )）。

关键点：函数变换法的核心在于变量替换与雅可比行列式的计算。

三、解题思路提炼与备考策略

1. 基础强化：构建知识网络

概念关联：例如，微分中值定理不仅用于证明不等式，还可结合积分中值定理解决极值问题。

公式推导：避免死记硬背，通过几何意义理解公式（如定积分的对称性）。

2. 题型归纳：分类训练与错题复盘

分类训练：将真题按考点归类（如极限计算、矩阵方程、随机变量分布），总结通用解法。

错题分析：记录解题中的逻辑漏洞，例如忽略矩阵不可逆的情况或概率密度函数的定义域。

3. 模拟实战：时间分配与心态调整

限时训练：每套真题控制在3小时内完成，逐步提升计算速度与准确率。

心态管理：通过模拟考试培养抗压能力，避免因复杂表达式产生畏难情绪。

四、结论

2014年数学三真题的解析表明，试题的命制始终围绕基础知识的深化与综合能力的考查。考生需以高频考点为核心，通过真题训练强化解题思维，同时注重知识体系的构建与跨章节综合应用能力的培养。唯有将理论分析与实战策略结合，才能在备考中实现从“量变”到“质变”的跨越。