模态逻辑作为形式逻辑的重要分支,在公职类考试、研究生入学考试及学科教育中占据关键地位。其核心命题围绕“必然”“可能”等模态词展开,强调对事物可能性与必然性的推理能力培养。本文结合近年真题及备考理论,探析模态命题的考查规律、解题逻辑与实用策略,为考生提供系统性指导。
一、模态命题的核心逻辑与分类体系
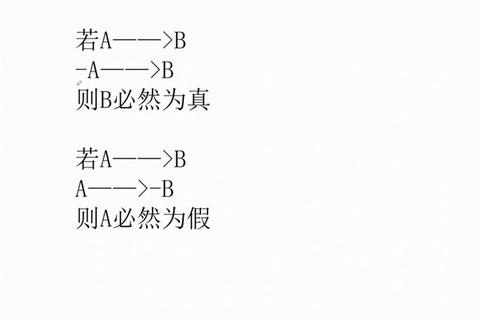
模态命题的核心在于通过逻辑词对命题真值范围进行限定。根据模态词性质,命题可分为四类:必然肯定命题(必然P)、必然否定命题(必然非P)、可能肯定命题(可能P)、可能否定命题(可能非P)。例如,“考试必然包含逻辑题”属于必然肯定命题,“改革可能不会立即生效”则属于可能否定命题。
四类命题间存在严密的对当关系,构成“模态方阵”:
1. 矛盾关系:必然P↔可能非P,必然非P↔可能P
(例:“他必然是凶手”与“他可能不是凶手”不可同真同假)
2. 反对关系:必然P与必然非P不可同真,但可同假
(例:“明天必然下雨”与“明天必然不下雨”至少一假)
3. 下反对关系:可能P与可能非P可同真,但不可同假
(例:“项目可能成功”与“项目可能失败”可并存)
4. 差等关系:必然命题蕴含可能命题
(例:“必然存在外星生命”可推出“可能存在外星生命”)
二、真题解析中的高频考点与陷阱规避
考点1:模态命题的等值转换
解题关键在于掌握否定词跨越模态词时的转换规则:
(例:“并非所有学生必然及格”等价于“有学生可能不及格”)
(例:“不可能所有人都迟到”等价于“必然有人不迟到”)
真题示例(2023年管理类联考):
题干:“并非所有灵长类动物大脑都具有额叶皮质。”
解析:转换为“有些灵长类动物大脑可能不具有额叶皮质”,对应选项A“不必然具有”。
考点2:复合模态推理的综合运用
需结合假言命题、直言命题进行多步骤推理。例如2022年国考真题:
题干:“巨额预算赤字必然导致贸易逆差?美国预算赤字最大但贸易顺差。”
解析:原命题为“必然P”,反例出现则等价于“可能非P”,故正确答案为“可能不会导致逆差”。
陷阱提示:
1. 语义偷换:混淆“可能不”与“不可能”(例:“可能没通过”≠“不可能通过”)
2. 范围误判:将“有些”等同于“所有”(例:“有些案件必然破获”不排除其他案件未破)
3. 双重否定失效:避免错误转换嵌套否定结构(例:“不必然不可能”应转换为“可能可能P”)
三、高效备考策略与思维训练方法
理论强化阶段:
1. 构建知识图谱:绘制模态方阵图,标注矛盾、反对等关系,辅以经典例题加深理解。
2. 公式记忆法:归纳“不必然=可能不”“不可能=必然不”等核心等式,形成条件反射。
3. 真题分类训练:按矛盾推理、复合模态等题型分类练习,记录高频错误类型。
实战提升阶段:
1. 语句结构拆解:将长句分解为“模态词+命题”结构。例如:
“并非所有参赛者都不可能晋级” → 否定词跨越“可能” → “有些参赛者可能晋级”。
2. 逆向思维训练:从选项反推题干逻辑,验证等价性(例:若选项含“必然非P”,则需题干出现“不可能P”)。
3. 限时模拟测试:设置15分钟完成10道模态题,培养快速识别关键词的能力。
思维误区纠正:
四、模态逻辑的跨学科应用与思维迁移
模态逻辑的训练不仅能提升应试能力,更可迁移至法律论证、商业决策等领域:
1. 法律文书分析:判断“证据必然有效”与“证言可能虚假”的对抗关系。
2. 风险评估模型:将“可能发生金融风险”量化为概率区间,辅助决策。
3. 学术研究设计:区分“理论必然成立”与“实验可能支持”的论证层次。
模态命题的掌握程度直接影响逻辑推理板块的得分效率。考生需从知识结构、解题技巧、思维模式三层面系统突破,通过“理论记忆—真题验证—错题复盘”的循环训练,将抽象逻辑规则转化为直观解题能力。随着公职考试对逻辑素养要求的提升,模态命题的深入理解不仅是应试需求,更是理性思维培养的重要基石。


