作为经济学与管理学领域的重要考核标杆,上海财经大学801经济学综合考试因其专业性强、知识覆盖面广而备受关注。如何在有限时间内精准把握核心考点、构建高效复习体系,是每位备考者的核心诉求。本文将从真题价值、高频考点拆解、科学复习方法论三大维度展开分析,助力考生在备考过程中实现事半功倍。
一、上海财大801真题的命题特征与备考价值
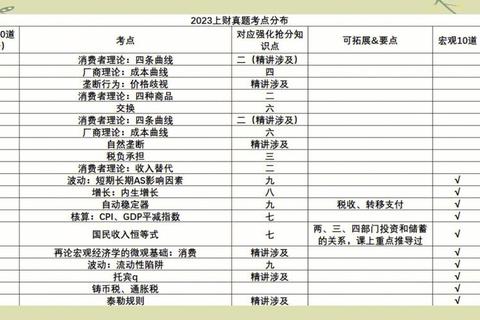
历年真题是研究考试命题逻辑的“金钥匙”。通过对近十年801真题的统计分析可以发现,微观经济学、宏观经济学与政治经济学的分值占比稳定在4:4:2,其中微观经济学注重消费者理论、生产者行为与市场结构分析,宏观经济学侧重经济增长模型、IS-LM框架与开放经济分析,而政治经济学则以劳动价值论、剩余价值理论为核心。值得注意的是,真题中约30%的题目会以变形题形式重复出现,例如2021年“垄断厂商定价策略”与2018年“价格歧视类型比较”均源于同一知识点。系统梳理真题不仅能识别高频考点,更能训练考生应对题型变化的逻辑迁移能力。
二、核心知识模块的深度解析与重难点突破

1. 微观经济学:模型构建与数理推导的双重挑战
消费者选择理论中,斯勒茨基分解与希克斯分解的对比分析是高频考点,考生需掌握替代效应与收入效应的图形推导及数值计算(如2020年真题要求用拉格朗日法求解最优消费组合)。生产者理论部分,成本曲线关系(短期与长期成本曲线、包络定理应用)及完全竞争市场长期均衡条件的动态分析是典型失分点。建议通过“三步法”强化:第一步绘制图形框架,第二步代入数学公式推导,第三步结合现实案例验证结论(如新能源补贴政策对厂商生产决策的影响)。
2. 宏观经济学:动态模型与政策分析的融合应用
索洛增长模型的稳态条件计算(如2022年真题要求推导黄金律储蓄率)、IS-LM模型在流动性陷阱场景下的政策有效性比较(参考2019年日本量化宽松案例)、蒙代尔-弗莱明模型与汇率制度的联动机制构成三大核心板块。复习时需建立“模型树”思维:以核心方程为中心(如Y=AK^αL^(1-α)),向外延伸参数变动的影响路径,并标注历年真题中出现的考查角度(如2021年考察技术进步率对稳态产出的影响)。
3. 政治经济学:理论逻辑与历史语境的辩证理解
劳动二重性、资本有机构成、利润率下降规律等概念需结合《资本论》原文进行语境化解读。例如,2023年真题要求用资本循环公式解释经济危机根源,答案需体现“货币资本-生产资本-商品资本”形态转化的矛盾性。建议制作“理论-现实对照表”,将抽象理论(如相对剩余价值生产)与当代案例(如人工智能对劳动时间压缩的影响)相关联,提升论述题的说服力。
三、四维复习策略:时间规划、工具选择与效能提升
1. 分阶段目标管理法
将备考周期划分为基础巩固(1-2个月)、专题强化(1个月)、模拟冲刺(3周)三阶段。基础阶段使用范里安《微观经济学》、曼昆《宏观经济学》教材搭建知识框架,配合思维导图梳理章节逻辑;强化阶段针对真题错题进行知识点溯源,建立“错题归因表”(标注错误类型:概念混淆/计算失误/模型理解偏差);冲刺阶段每周完成一套限时模拟,重点训练计算题答题规范(如推导过程分步书写)与论述题答题结构(论点+理论依据+实例论证)。
2. 高效学习工具组合
知识图谱工具:使用XMind绘制跨章节知识关联图(如将微观生产函数与宏观增长模型联结),可视化呈现交叉考点。
记忆辅助系统:基于艾宾浩斯遗忘曲线设计复习节点,对核心公式(如柯布-道格拉斯效用函数的边际替代率)进行间隔重复记忆。
数据化进度管理:利用Notion建立复习日志,量化每日学习时长、章节完成度及正确率变化趋势,动态调整复习重点。
3. 应试技巧的精雕细琢
计算题“三查法”:一查单位换算(如名义变量与实际变量转换)、二查导数计算符号、三查经济意义合理性(如需求弹性绝对值是否大于1)。
论述题“金字塔结构”:采用“总-分-总”框架,首段明确核心观点,中间分点论述(每点包含理论+公式+案例),结尾总结政策启示或理论局限性。例如分析最低工资政策效应时,可先陈述完全竞争市场与买方垄断市场的不同影响,再引入Card&Krueger(1994)的实证研究增强论证层次。
4. 心理调适与资源整合
组建3-5人备考小组进行模拟答辩,针对争议性问题(如凯恩斯主义与新古典学派的政策分歧)开展角色辩论,既能深化理解又可缓解焦虑。同时关注上海财大经济学院官网的学术动态,近年真题常涉及诺贝尔经济学奖得主研究成果(如2021年引用契约理论解释信息不对称问题)。
从知识复现到思维跃迁的质变之路
上海财大801经济学考试的竞争本质,是考查考生能否将经济学原理转化为分析现实问题的思维工具。通过真题驱动的考点解析、模块化的知识重构以及科学复习策略的落地执行,考生不仅能系统掌握考核要点,更能培养起“模型化思考、实证化验证”的经济学素养——这种能力将成为未来学术研究或职业发展的底层竞争力。正如萨缪尔森所言:“优秀的经济学思维,始于严谨的模型训练,终于对复杂世界的简洁解释。”


