全微分考点解析_考研数学真题精讲与典型例题突破

全微分作为多元函数微分学的核心内容，是考研数学（一）、数学（二）和数学（三）的必考知识点之一。其在解决几何、物理、经济等应用问题中具有重要作用，同时与隐函数、复合函数求导等知识点紧密关联。本文通过梳理历年真题与典型例题，结合备考策略，帮生系统性掌握全微分的核心考点与解题技巧。

一、全微分的基本概念与考纲要求

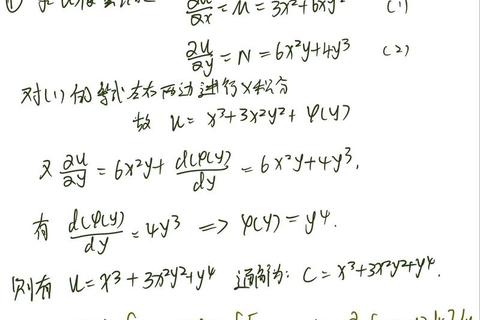
全微分是多元函数微分学的基础，考纲明确要求考生“理解全微分的概念，掌握全微分的计算方法，了解全微分存在的必要条件和充分条件”。其数学定义为：若函数 ( z = f(x, y) ) 在点 ( (x_0, y_0) ) 处的全增量 ( Delta z ) 可表示为 ( Delta z = ADelta x + BDelta y + o(rho) )，其中 ( A, B ) 与 ( Delta x, Delta y ) 无关，( rho = sqrt{(Delta x)^2 + (Delta y)^2} )，则称 ( ADelta x + BDelta y ) 为函数在点 ( (x_0, y_0) ) 处的全微分，记为 ( dz = A dx + B dy )。

关键点：

1. 必要条件：若 ( f(x, y) ) 在点 ( (x_0, y_0) ) 处可微，则其在该点的偏导数 ( frac{partial z}{partial x} ) 和 ( frac{partial z}{partial y} ) 必存在，且 ( dz = frac{partial z}{partial x} dx + frac{partial z}{partial y} dy )。

2. 充分条件：若偏导数在点 ( (x_0, y_0) ) 处连续，则函数在该点可微。

二、全微分的解题方法与典型例题

方法1：直接求导法

步骤：

1. 分别求出函数对 ( x ) 和 ( y ) 的偏导数 ( frac{partial z}{partial x} ) 和 ( frac{partial z}{partial y} )；

2. 代入全微分公式 ( dz = frac{partial z}{partial x} dx + frac{partial z}{partial y} dy )。

真题示例（2015年数学二真题）：

设 ( z = e^{x+y} + sin(xy) )，求全微分 ( dz )。

解析：

计算偏导数：

( frac{partial z}{partial x} = e^{x+y} + ycos(xy) )，

( frac{partial z}{partial y} = e^{x+y} + xcos(xy) )。

代入公式得：

( dz = left( e^{x+y} + ycos(xy) right) dx + left( e^{x+y} + xcos(xy) right) dy )。

关键点：直接法适用于显函数形式，需注意复合函数求导时的链式法则。

方法2：隐函数全微分法

适用场景：当函数以隐式方程 ( F(x, y, z) = 0 ) 形式给出时，需对方程两边同时求全微分。

步骤：

1. 对隐方程两边求全微分，展开后整理为 ( A dx + B dy + C dz = 0 )；

2. 解出 ( dz ) 表达式。

例题（改编自2015年数学一真题）：

设方程 ( x^2 + y^2 + z^2

2xyz = 1 ) 确定隐函数 ( z = f(x, y) )，求全微分 ( dz )。

解析：

对方程两边求全微分：

( 2x dx + 2y dy + 2z dz

2(yz dx + xz dy + xy dz) = 0 )。

整理得：

( dz = frac{(yz

x) dx + (xz

y) dy}{z - xy} )。

关键点：隐函数求导需注意变量间的对称性，并正确应用乘积法则。

三、全微分的常见题型与易错点

题型1：结合极限与连续性的综合题

例题：设 ( f(x, y) = begin{cases}

frac{xy}{sqrt{x^2 + y^2}} & (x, y)

eq (0, 0)

0 & (x, y) = (0, 0)

end{cases} )，讨论 ( f(x, y) ) 在 ( (0, 0) ) 处的可微性。

解析：

验证偏导数是否存在：计算 ( frac{partial f}{partial x}(0, 0) = lim_{h

o 0} frac{f(h, 0)

f(0, 0)}{h} = 0 )，同理 ( frac{partial f}{partial y}(0, 0) = 0 )。

检验可微性：计算极限

( lim_{rho

o 0} frac{f(h, k)

[f(0, 0) + 0 cdot h + 0 cdot k]}{sqrt{h^2 + k^2}} = lim_{(h, k) o (0, 0)} frac{hk}{h^2 + k^2} )，该极限不存在，故不可微。

易错点：考生易混淆“偏导数存在”与“可微”的关系，忽略充分条件的验证。

题型2：几何与物理应用

真题示例（2024年数学二真题）：

已知曲面 ( z = x^2 + y^2 ) 在点 ( (1, 1, 2) ) 处的切平面方程为 ( ax + by + cz = d )，求 ( a, b, c, d )。

解析：

计算全微分得法向量：

( dz = 2x dx + 2y dy )，即法向量为 ( (2x, 2y, -1) )。

代入点 ( (1, 1, 2) )，法向量为 ( (2, 2, -1) )，故切平面方程为 ( 2(x

1) + 2(y - 1) - (z - 2) = 0 )，化简得 ( 2x + 2y - z = 2 )。

关键点：全微分与几何应用结合时，需将法向量与切平面方程关联。

四、备考策略与真题训练建议

1. 基础巩固：

熟练掌握偏导数、链式法则及隐函数求导规则。

通过《复习全书·基础篇》系统梳理知识点，结合660题训练计算能力。

2. 真题精练：

重点练习2015年、2021年及2024年真题中的全微分题目，分析命题趋势。

使用微分算子法优化隐函数求导步骤，提升解题效率。

3. 易错总结：

建立错题本，记录混淆点（如“可导”与“可微”的区别）及复杂隐函数处理技巧。

五、

全微分作为多元微分学的核心工具，其考点贯穿于几何、物理及经济应用问题中。考生需通过理论深化与真题实战相结合，掌握直接求导法与隐函数法的精髓，同时注重易错点的归纳。在备考中，建议以《复习全书》为基础，辅以历年真题的针对性训练，最终实现解题能力的质变与考分的突破。