在材料力学与结构力学考研中,弯矩图的绘制与分析是核心考点之一,其重要性贯穿于静定结构内力分析、强度校核及变形计算等多个环节。无论是简支梁、悬臂梁还是复杂刚架系统,弯矩图均是解题的关键工具。本文结合历年考研真题与典型例题,系统梳理弯矩图的考查形式、解题逻辑与常见误区,为考生提供理论与实操并重的备考指南。
一、弯矩图的考查意义与题型分类
弯矩图是梁或刚架各截面弯矩分布规律的图形化表达,其本质是结构受力与变形关系的直观呈现。在考研中,弯矩图的考查意义主要体现在三个方面:
1. 基础能力检验:通过弯矩图绘制,考查考生对截面法、平衡方程、载荷与弯矩微分关系的掌握程度。
2. 综合应用衔接:弯矩图是后续强度校核(如正应力计算)、位移分析(如图乘法应用)及超静定问题求解的基础。
3. 工程思维训练:合理弯矩分布与结构设计直接相关,如确定危险截面、优化构件尺寸等。
典型考研题型分类:
二、弯矩图绘制的核心步骤与技巧
(一)绘制流程:从支反力到图形成型
1. 计算支反力:通过整体平衡方程(ΣF_y=0, ΣM=0)求解支座约束力。
2. 分段与截面法:根据载荷突变点(集中力作用点、分布载荷起止点、支座处)将梁分段,逐段计算弯矩值。
3. 图形绘制规则:
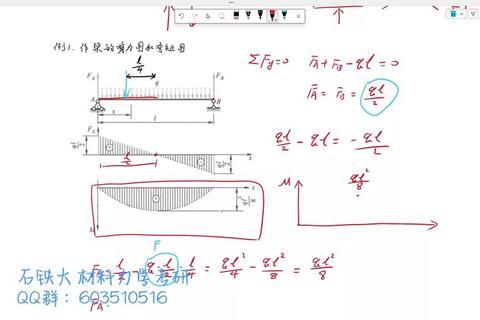
示例分析(以简支梁受均布载荷为例):
1. 计算支反力:由对称性可得两端支反力均为qL/2。
2. 取距左端x的截面,弯矩方程为M(x)= (qL/2)x
3. 图形为开口向下的抛物线,跨中弯矩最大值为qL²/8。
(二)提速技巧:规避常见计算陷阱
1. 符号快速判定法:
2. 对称性利用:对称结构在对称载荷下弯矩图必对称,可减少计算量。
3. 特殊点记忆:
三、真题高频难点与突破策略
(一)复杂刚架系统弯矩图绘制
难点:刚架存在多个杆件与节点,需同时考虑轴力、剪力与弯矩的耦合效应。
解题策略:
1. 拆分结构:将刚架分解为单杆分析,注意节点处的弯矩平衡(如刚节点弯矩守恒)。
2. 从静定部分入手:优先计算附属部分的内力,再传递至基本部分。
3. 校核关键点:检查刚节点处弯矩是否满足ΣM=0,避免累计误差。
例题参考(三铰刚架受水平力):
1. 利用铰接点弯矩为零的特性,列平衡方程求支反力。
2. 分别绘制横梁与立柱的弯矩图,注意立柱的弯矩线性分布特性。
(二)移动载荷下的最不利弯矩分析
考查形式:确定载荷位置使指定截面弯矩最大(如桥梁设计中车辆载荷的影响)。
解题方法:
1. 影响线法:绘制指定截面的弯矩影响线,确定载荷最不利位置。
2. 极值定理:对弯矩函数求导,找到载荷作用位置的极值点。
四、备考建议与常见误区警示
(一)系统性训练规划
1. 阶段一(基础巩固):
2. 阶段二(综合提升):
3. 阶段三(冲刺模拟):
(二)典型错误案例分析
1. 支反力计算错误:未考虑力偶对支反力的影响,导致后续弯矩全盘错误。
2. 符号混淆:将材料力学与结构力学的弯矩正负约定混用。
3. 图形比例失真:抛物线曲率绘制不当,导致极值点位置误判。
五、
弯矩图的掌握程度直接关系材料力学与结构力学考研的成败。考生需从基础规则入手,通过阶梯式训练逐步攻克复杂题型,同时注重真题规律总结与错题归因分析。面对综合题时,应善用对称性、叠加原理等工具提升效率,最终实现从“会画图”到“精分析”的能力跃迁。


