在电气工程领域,电路理论是构建专业能力的基石。作为华中科技大学研究生入学考试的核心科目之一,电路真题不仅是知识水平的试金石,更是考生洞察命题规律、提升解题效率的战略工具。本文将深入解析华中科技大学电路考试的核心考点与典型题型,结合科学备考策略,为考生提供兼具理论深度与实践价值的指导方案。
一、核心考点的逻辑框架与命题特征
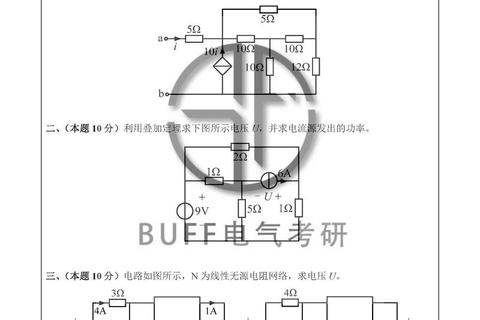
华中科技大学电路真题始终围绕三大核心模块展开:基础电路定律与定理、动态电路分析与频域分析技术。这三大模块构成命题的"铁三角",覆盖了90%以上的分值权重。
1. 基础电路定律与定理
基尔霍夫定律、戴维南-诺顿定理、叠加定理等基础内容看似简单,实则暗藏命题陷阱。例如2021年真题中,通过构造含受控源的复杂网络,要求考生综合运用节点电压法与戴维南定理,检验对定理适用条件的理解深度。此类题型的解题关键在于:识别等效变换的边界条件,避免机械套用公式。
2. 动态电路分析
一阶、二阶动态电路的时域分析是区分考生能力的重要标尺。典型题型如2020年考题:给定RLC串联电路的阶跃响应曲线,要求反推电路参数。此类题目需掌握"三要素法"的进阶应用,特别注意初始储能对响应曲线形态的影响。建议通过绘制状态变量变化图辅助分析。
3. 频域分析技术
正弦稳态电路、谐振现象及滤波器设计构成频域分析的"黄金三角"。2022年真题中的三相电路不对称故障分析题,要求考生在频域与时域之间灵活切换思维,这提示备考需建立复数域与时间域的映射关系认知框架。
二、典型题型的解题范式与思维突破
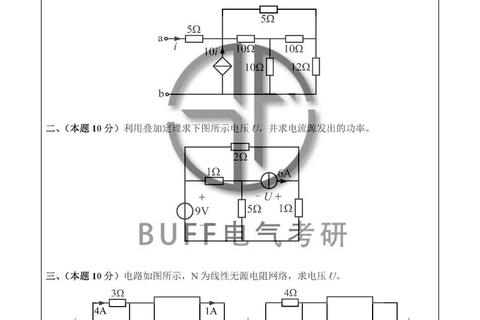
通过分析近五年真题,可将高频题型归纳为四类,每种类型对应特定的解题方法论:
类型1:多定理综合应用题
例题特征:含多个独立源、受控源的线性网络,要求计算特定支路参数。
破题策略:
类型2:动态电路参数反推题
例题特征:给定响应曲线或特定时刻的电压/电流值,求电路元件参数。
破题要点:
类型3:频域综合设计题
典型例题:设计满足特定幅频特性的无源滤波器。
方法论框架:
1. 根据截止频率选择滤波器类型(巴特沃斯/切比雪夫)
2. 利用归一化频率进行参数换算
3. 通过品质因数Q值调整通带平坦度与阻带衰减速度
类型4:非线性电路分析题
命题趋势:近年来对二极管、运放等非线性元件的考查比例上升。
解题技巧:
三、从真题解析到备考策略的实践转化
科学的备考策略应实现"知识网络构建"与"解题能力提升"的协同进化,建议采用三阶段递进式方案:
阶段1:考点图谱构建(4周)
阶段2:题型专项突破(6周)
阶段3:全真模拟与策略优化(2周)
四、命题趋势研判与前瞻性准备
通过对2023年最新真题的解析,可以发现两个显著趋势:
1. 工程实践导向强化:出现电力电子开关电路瞬态分析等交叉学科内容
2. 计算复杂度控制:减少纯数值计算,增加对物理意义的解释要求(如要求用能量守恒原理解释谐振现象)
应对策略建议:
构建电路分析的元认知体系
电路真题的破解之道,本质在于建立"理论-方法-实践"的元认知框架。考生应超越对单一知识点的机械记忆,转而培养"电路拓扑解析→数学模型建立→物理意义阐释"的系统思维能力。这种能力的形成,不仅关乎考试成败,更将成为未来解决复杂工程问题的核心素养。当每一道真题的解析过程都转化为认知升级的阶梯,成功便不再是偶然的运气,而是水到渠成的必然。


