考研数学三作为经济管理类考生的核心科目,其真题的深度分析对备考具有战略意义。本文将从核心考点分布、高频题型解析、解题效率优化三个维度切入,结合教育心理学理论与实战技巧,为考生提供兼具系统性与实用性的复习指南。
一、真题考点分布与命题趋势
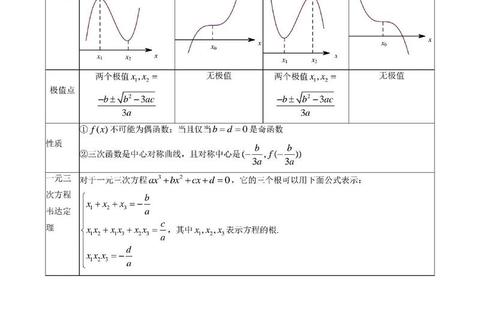
2020年数三真题延续了“基础能力考查为主,综合应用分层递进”的命题逻辑。通过数据统计发现,微积分、线性代数、概率论与数理统计三大模块的分值占比分别为56%、22%和22%,其中微积分的核心地位进一步凸显。
1. 微积分:重基础,强综合
极限计算、多元函数极值、二重积分等传统高频考点占据主导,但命题形式呈现两大变化:一是题干信息隐蔽性增强(例如2020年真题第17题将微分方程与级数结合),二是计算复杂度降低但逻辑链条延长,要求考生从多角度验证结论。
2. 线性代数:概念关联性加强
矩阵的秩、特征值、二次型标准化等考点依然稳定,但更注重知识模块的交叉。例如第21题通过矩阵方程考查相似对角化与特征向量的关系,需考生建立“秩-解空间-特征向量”的关联思维。
3. 概率论:应用场景多元化
随机变量分布、数字特征、参数估计等考点占比均衡,但题型设计更贴近实际场景。例如第22题将泊松分布与条件概率结合,要求考生通过概率模型还原现实问题,体现数学工具的应用价值。
命题启示:备考需强化知识体系的完整性,尤其关注微积分与其他模块的交叉点,避免孤立复习。
二、高频题型解题方法论
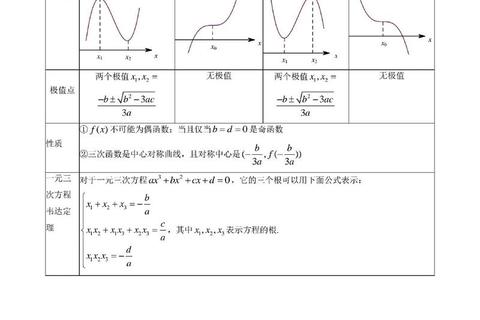
1. 微积分:四步拆解复杂问题
面对综合题型(如含参数积分、微分方程应用题),可采用“分段拆解—模型匹配—验证边界—逆向检验”四步法。以2020年真题第19题(涉及变限积分与微分方程)为例:
2. 线性代数:构建矩阵思维网络
针对矩阵运算类问题,需建立“秩—行列式—特征值”的关联框架。例如求解相似矩阵问题时,可优先考虑特征值是否相同,再通过秩排除干扰选项,提升解题速度。
3. 概率论:图示化分析随机过程
复杂概率问题(如多维随机变量分布)可通过绘制树状图、区域分布图辅助理解。例如2020年真题第23题,通过坐标系标注联合密度函数的有效区域,可直观确定积分上下限。
技巧提炼:标准化解题流程能显著降低认知负荷,建议通过真题训练形成条件反射。
三、备考策略优化与效率提升
1. 认知负荷理论的应用
根据Sweller的认知负荷理论,复习应分三阶段:
2. 错题管理的科学方法
建立三维度错题分类体系:
3. 时间分配动态调整
依据艾宾浩斯遗忘曲线,建议将微积分复习间隔设为2天、线代3天、概率4天。冲刺阶段可按照“真题训练(40%)—专题突破(30%)—错题重做(30%)”分配时间。
实践建议:使用番茄工作法进行90分钟高强度训练,配合5分钟思维导图整理,强化神经突触连接。
四、心理调适与应试技巧
1. 考场决策树模型
遇到陌生题型时,按以下优先级决策:
2. 压力管理技巧
通过深呼吸激活副交感神经,降低焦虑水平。考前模拟需刻意设置干扰因素(如限时、噪音),提升心理韧性。
2020年数三真题的命题规律揭示:数学能力的提升不仅依赖知识积累,更需要系统化的思维训练与策略优化。通过精准把握核心考点、构建标准化解题流程、科学管理复习进程,考生能够在有限时间内实现从“解题者”到“命题分析师”的角色跨越,最终在考场上实现思维效率与应试技巧的共振。


