机械原理作为机械工程学科的核心基础课程,既是理论研究的基石,也是工程实践的关键工具。对于报考武汉大学机械类研究生的考生而言,深入理解其命题规律与知识体系,是突破考试瓶颈的核心路径。本文基于近年真题解析,结合教学实践经验,系统阐述备考策略与知识框架构建方法,助力考生实现科学备考。
一、武汉大学机械原理命题特征与核心考点剖析
武汉大学机械原理真题具有“重基础、强综合、考思维”的特点。通过分析2010年、2004年等典型年份试题(如四杆机构设计、轮系传动比计算、齿轮变位修复等题目),可提炼出四大核心模块:
1. 平面机构分析与设计
高频考点包括自由度计算(如复合铰链识别)、速度瞬心法应用、连杆机构综合设计(如给定行程速比系数的铰链四杆机构求解)等。例如2023年真题中出现的“曲柄摇杆机构急回特性分析”,要求考生结合极位夹角与行程速比系数的关系推导几何参数。解题时需掌握“杆长条件+几何作图法”双重验证技巧,避免因忽略极限位置几何约束而失分。
2. 齿轮传动与轮系计算
涉及变位齿轮修复(如负变位量计算)、斜齿轮参数换算、行星轮系传动比求解等难点。典型如2010年试题中,要求根据中心距反推模数与齿数,并设计高变位齿轮的齿顶圆直径。此处需综合应用齿顶高公式$d_a=m(z+2h_a^+2x)$与等移距变位条件$x_1=-x_2$,特别注意变位系数对齿顶圆尺寸的影响。
3. 凸轮机构与动力学分析
涵盖压力角优化、从动件运动规律设计(如余弦加速度曲线的刚性冲击判断)等内容。真题中常出现“基圆半径确定”“最大升程计算”等题型,需掌握反转法作图与运动线图叠加技巧。例如2020年真题要求绘制偏置滚子从动件凸轮廓线,需通过偏心距修正确定理论廓线与实际廓线差异。
4. 机械效率与速度波动调节
重点考查自锁条件判定、飞轮转动惯量计算等。考生需熟练运用摩擦角原理分析斜面机构自锁,并理解等效转动惯量公式$J=frac{W_{max}}{omega^2[delta]}$中各参数的物理意义。如2018年试题中,通过能量累积图计算飞轮惯量时,需注意最大盈亏功的周期划分。
二、典型题型突破策略与解题方法论
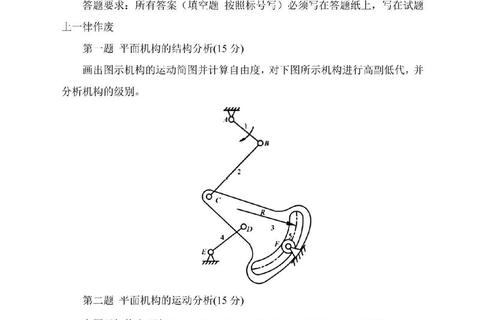
1. 概念辨析类题型
选择题与判断题侧重考察知识盲点,如“渐开线齿廓啮合特性”“运动副等效代换原则”等。建议采用“关键词锚定法”:针对“基圆半径决定齿廓形状”“当量摩擦角计算”等易混淆概念,建立对比表格(如表1),通过真题错题归纳高频陷阱。
表1 机械原理易混淆概念对比
| 概念 | 核心要点 | 典型错误 |
||||
| 压力角与传动角 | 压力角α+传动角γ=90° | 误将压力角视为机构位置函数 |
| 瞬心与速度方向 | 瞬心为等速重合点,方向垂直连线 | 混淆绝对瞬心与相对瞬心速度关系 |
2. 计算分析类题型
针对轮系传动比、机构自由度等计算题,推荐“三步验证法”:
例如行星轮系计算中,若求得传动比绝对值大于10,需反向验证中心轮齿数是否满足同心条件。
3. 综合设计类题型
四杆机构设计、凸轮廓线绘制等题目需融合图解与解析法。以“给定行程速比系数K的机构设计”为例,可遵循以下流程:
1) 由$K=frac{180°+θ}{180°-θ}$计算极位夹角θ
2) 选取固定铰链位置,作极位几何辅助圆
3) 利用圆心角2θ确定活动铰链轨迹
4) 校验最小传动角γ_min≥40°的可行性
三、系统性备考策略与资源整合
1. 三阶段复习法
2. 真题深度利用技巧
3. 辅助工具与资源推荐
四、
武汉大学机械原理考试既是对知识体系的检验,更是对工程思维能力的考核。通过“考点图谱构建—解题模型提炼—仿真验证强化”的三维学习框架,考生可有效突破知识断层。建议在最后备考阶段,每日进行2小时的全真模拟,培养高强度解题耐力,同时注重答题规范性训练(如齿轮参数的标准书写格式),最终实现从知识积累到应试能力的质变提升。


