考研数学真题作为衡量考生能力与命题趋势的权威载体,始终是备考策略制定的核心依据。 对于数百万考生而言,深入理解历年试题的难易波动规律与演变方向,不仅能够优化复习路径,更能精准把握命题逻辑背后的潜在意图。本文将从真题难度特征、周期变化规律、命题趋势解读及实战应对策略四个维度展开系统分析,为考生构建科学备考框架提供理论支撑与实践指导。
一、历年真题难度特征的多维解析

考研数学试题的“难度”并非单一维度的概念,而是由知识覆盖广度、计算复杂度、思维跳跃性三重指标共同构成。以2015年至2023年的真题为例,线性代数模块的难度波动显著:2017年首次出现“矩阵相似与二次型结合证明题”,因需要跨章节知识融合,当年该题正确率不足30%;而2021年同类型题目通过降低抽象性(如引入具体数值矩阵)使得分率提升至55%。这揭示命题组在平衡“区分度”与“基础性”时的动态调整策略。
从学科模块视角观察,高等数学始终占据难度峰值,尤其在中值定理证明、级数收敛性判定、曲线曲面积分计算三类题型中,历年平均失分率超过40%。反观概率论与数理统计模块,其难度呈现“阶梯式上升”特征,2018年后逐渐增加假设检验与参数估计的实际应用题比例,要求考生从公式套用转向问题建模能力的突破。
二、试题难易周期的“五年定律”与外部影响因素
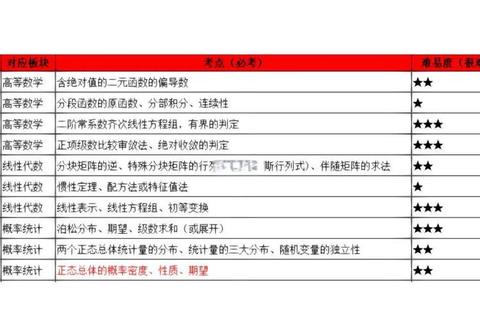
通过统计近20年真题难度系数(计算公式:1
值得注意的是,奇数年与偶数年的“难度交替说”缺乏数据支撑。2020年(偶数年)数一试卷因涉及“傅里叶级数展开结合热传导方程”的创新题型,难度系数达到0.68,显著高于2019年的0.72(系数越低代表难度越高)。这提示考生需摒弃经验主义,转向基于真题大数据的动态分析。
三、命题趋势的三大转向与应对逻辑
当前考研数学命题正经历“去技巧化、强基础性、重思维链”的范式转型,具体表现为:
1. 计算题从“量”到“质”的升级:2022年数二真题中,一道定积分计算题融合了分部积分、变量代换、对称性分析三重步骤,看似常规却暗含逻辑陷阱,单纯依赖“刷题套路”的考生易陷入计算冗余而超时。
2. 证明题从“形式化”到“思想性”的进化:传统的中值定理证明多依赖固定辅助函数构造,而2023年真题要求通过函数形态分析自主选择证明工具(如泰勒展开与罗尔定理的组合应用),侧重数学直觉的培养。
3. 应用题从“学科交叉”到“现实渗透”的深化:近三年经济类真题频繁出现“供应链优化”“风险评估”等场景,要求考生在10分钟内完成从文字到数学表达的转化,这对信息提取与抽象思维能力提出更高要求。
针对上述趋势,备考策略需遵循“三阶递进”原则:第一阶段通过近十年真题完成知识点漏洞扫描(建议使用“错题溯源法”标记薄弱环节);第二阶段聚焦2015年后的改革期真题,重点突破综合题型的时间分配与思维转换;第三阶段模拟近三年真题环境,训练在高压情境下快速调用“解题思维树”的能力。
四、从真题分析到实战落地的四维策略
1. 题型解构工具化:建立“题型-考点-难度”三维对照表,例如将级数收敛性判别细分为“定义法”“比较法”“积分法”等子类,并标注近五年考察频次与错误率数据。
2. 时间配置弹性化:根据2023年考生调研,得分超过120分的群体普遍采用“4-3-3”时间分配模型:40分钟完成选择填空(预留15分钟复查),90分钟主攻大题(其中30分钟专攻1-2道压轴题),剩余时间用于公式复查与策略调整。
3. 思维误区清单化:整理高频认知陷阱,如“格林公式使用忽视单连通区域条件”“泊松分布与二项分布混用”等,在冲刺阶段进行定向排除。
4. 心理韧性场景化:通过限时完成2016年、2020年等高难度真题,模拟考场突发压力,培养“暂时性卡顿跳过-后续回溯”的决策能力。
真题难度的波动本质是命题逻辑与人才选拔需求的镜像反映。考生唯有超越“就题论题”的浅层分析,转而从历史数据中提炼规律,从趋势演变中预判重点,从策略迭代中构建比较优势,方能在激烈竞争中实现从“知识存量”到“应用效能”的质变突破。正如控制论中的“负反馈调节”原理:持续将真题训练中的误差信号转化为认知系统的升级动力,正是通往高分的终极密码。


