作为考研数学中难度较高、覆盖面最广的科目,数学一不仅要求考生掌握扎实的理论基础,还需具备灵活运用知识解决复杂问题的能力。2013年考研数学一真题在延续历年命题规律的也凸显了一些值得深入研究的核心考点与典型题型。本文将从高频考点解析、典型题型拆解及备考策略优化三个维度展开分析,帮生建立系统化复习框架,提升解题效率。
一、核心考点的分布规律与命题逻辑

数学一的命题始终围绕高等数学、线性代数、概率论与数理统计三大模块展开,但不同年份对各部分的考查侧重点有所不同。2013年真题中,以下知识点尤为突出:
1. 高等数学:极限与积分的综合应用
极限与积分是高等数学的基础,2013年真题中多道题目通过结合泰勒展开、变限积分等技巧,考查考生对极限存在性、收敛性及积分计算方法的掌握。例如,填空题中出现的“利用夹逼定理求解极限”题目,要求考生不仅熟悉定理本身,还需灵活构造不等式进行推导。
2. 线性代数:矩阵的秩与线性方程组解的结构
矩阵的秩是线性代数中的核心概念,2013年真题中多次出现通过矩阵秩的变化分析方程组解的情况。例如,一道解答题要求考生根据矩阵秩的约束条件,判断线性方程组是否有解,并讨论解的表达式。此类题目需考生深入理解秩与解空间维度的关系。
3. 概率论:多维随机变量分布与数字特征
2013年真题在概率论部分重点考查了二维随机变量的联合分布、边缘分布及协方差计算。例如,一道解答题以连续型随机变量为背景,要求考生通过积分变换求解联合概率密度函数,并进一步计算相关系数。这要求考生熟练掌握概率密度函数的转换方法及数字特征的积分表达。
命题逻辑启示:数学一真题强调知识点的交叉融合。例如,微积分与线性代数结合(如利用矩阵求解微分方程)、概率论与积分变换结合(如通过傅里叶变换求解概率分布)等。考生需打破学科界限,建立知识网络。
二、典型题型的解题思路与技巧拆解
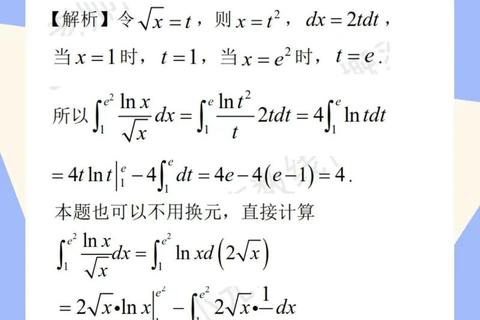
针对2013年真题中的代表性题目,以下分析其解题关键步骤与易错点:
例题1(高等数学)
题目:计算定积分 (int_{0}^{1} frac{x ln(1+x)}{1+x^2} , dx)。
解析:
例题2(线性代数)
题目:已知矩阵(A)为3阶实对称矩阵,且(A^2 = 2A),求矩阵(A)的秩。
解析:
例题3(概率论)
题目:设二维随机变量((X,Y))服从区域(D: 0 leq x leq 1, 0 leq y leq x)上的均匀分布,求(E(XY))。
解析:
三、科学备考策略与资源优化建议
1. 分阶段复习规划
2. 高效利用真题与工具
3. 避免常见误区
2013年考研数学一真题体现了命题组对考生综合能力的一贯要求:既要精通基础理论,又需具备跨章节整合知识、快速识别解题突破口的能力。通过系统梳理核心考点、拆解典型题型,并结合科学的备考策略,考生可显著提升复习效率,在考场上从容应对各类挑战。最终,数学能力的提升不仅关乎考试分数,更是逻辑思维与问题解决能力的终身积淀。


