工程力学作为理工科考研的核心科目之一,其真题解析与核心考点掌握是考生备考的关键。本文将从学科特点、核心考点剖析、典型题型精讲及备考策略四个维度展开,结合近年真题案例与教育理论,为考生提供系统化的复习指导。
一、工程力学考研的学科特点与命题趋势
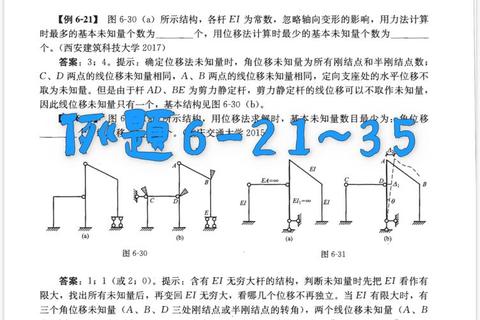
工程力学包含理论力学(静力学、运动学、动力学)与材料力学两大模块,其命题注重基础理论与工程应用的结合。近年真题呈现以下趋势:
1. 题型多样化:填空题侧重概念辨析(如“力偶矩的计算”“柔度系数”),选择题聚焦受力分析与材料特性判断,计算题涵盖梁的内力图、强度校核及动力学综合问题。
2. 综合性强:如2023年武汉科技大学真题中,材料力学大题首次引入“挠曲线方程”,要求考生在掌握弯矩图的基础上推导变形,体现跨知识点融合。
3. 实践导向:压杆稳定性、组合变形等考点常结合工程案例(如机械零件设计、结构优化)命题,强调解决实际问题的能力。
二、核心考点剖析与高频题型

(一)静力学与运动学
1. 静力学平衡分析
2. 运动学综合问题
(二)材料力学与强度理论
1. 内力图与应力分析
2. 组合变形与能量法
三、典型题型精讲与解题技巧
案例1:静力学平衡问题(武汉科技大学2015年真题)
题目:图示结构中,已知q=10kN/m,M=10kN·m,求A、B、C处的约束力。
解析步骤:
1. 拆解结构:将梁分为AC与CB段,分别取隔离体。
2. 对CB段列平衡方程:ΣMc=0 → F_B·L
3. 对AC段分析:利用作用力与反作用力关系,结合ΣFy=0与ΣMA=0求解F_A与F_C。
技巧提示:优先选择力矩方程以减少未知数数量,注意分布载荷的等效集中力处理。
案例2:材料力学强度校核(厦门大学2023年真题)
题目:槽形截面梁受均布载荷q=15kN/m,校核其正应力强度。
关键步骤:
1. 绘制剪力图与弯矩图,确定危险截面(通常为弯矩最大或截面突变处)。
2. 计算截面惯性矩Iz及形心位置,校核拉应力(σ_t≤[σ_t])与压应力(σ_c≤[σ_c])。
3. 注意中性轴位置对拉压区的影响,如D截面下缘压应力最大。
易错点:忽略截面几何不对称性导致的应力分布差异。
四、高效备考策略与资源推荐
1. 分阶段复习法
2. 资源工具推荐
3. 应试技巧
五、
工程力学考研的核心在于系统性理解与精准应用。通过剖析真题规律、强化核心考点训练,并结合科学的备考策略,考生可显著提升解题效率与准确率。建议考生在复习中注重“理论-题型-实践”的三维联动,善用优质资源,最终实现从知识积累到应试能力的跨越式突破。


