把握命题脉络，提升备考效率——2017年考研数学二真题深度解析

作为研究生入学考试的核心科目之一，数学二因其对基础知识的深度考查与综合应用能力的高要求，成为众多理工科考生备考的“分水岭”。通过对2017年考研数学二真题的系统解析，不仅能帮生厘清高频考点与命题规律，更能为后续备考提供科学的策略指导。本文将从核心考点分布、典型题型解析及备考建议三方面展开，结合真题实例与教育理论，为考生构建清晰的复习框架。

一、核心考点分布：聚焦高频板块，明确复习重心

2017考研数学二真题解析_核心考点分布与典型题型精讲

2017年数学二真题延续了“重基础、强综合”的命题风格，核心考点集中在高等数学的微积分、线性代数的基础理论与应用两大模块。具体分布如下：

1. 微积分板块（占比约80%）

  • 极限与连续：重点考查极限计算（如等价无穷小替换、洛必达法则）及连续性判定，题目多与函数性质结合。
  • 一元函数微分学与积分学：微分中值定理的应用（如罗尔定理证明题）、定积分几何应用（旋转体体积计算）为高频题型。
  • 多元函数微分学：偏导数计算与极值问题出现频次较高，需注意隐函数求导与条件极值的综合应用。

    • 2. 线性代数板块（占比约20%）

  • 矩阵与行列式：矩阵的秩、行列式性质及计算是基础考查点。
  • 向量与线性方程组：向量组的线性相关性、齐次方程组解的结构为命题重点，常结合矩阵运算综合命题。

    • 命题趋势解读：2017年真题体现出对考生“计算能力”与“逻辑推导能力”的双重考查。例如，微分方程与积分的结合题要求考生灵活运用公式变形，而线性代数中矩阵秩的讨论则需严谨的逻辑链条支撑。

    二、典型题型精讲：拆解解题逻辑，提炼方法模板

    2017考研数学二真题解析_核心考点分布与典型题型精讲

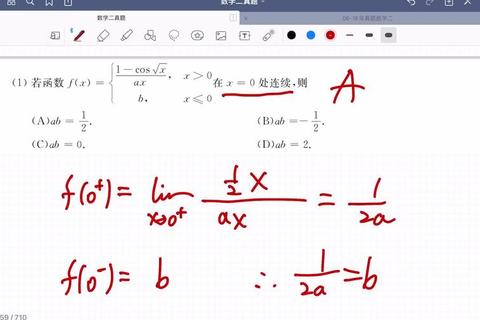
    真题解析的核心在于归纳解题思路，将复杂问题转化为可复用的方法模板。以下选取两类典型题型进行精讲：

    1. 极限计算题——化繁为简的核心技巧

    例题（2017年第1题）：计算极限 (lim_{x

    o 0} frac{e^x

  • sqrt{1+2x}}{x^2})。

    • 解题步骤：

  • 步骤一：识别极限类型（0/0型），优先尝试泰勒展开。将分子展开至二阶：(e^x = 1 + x + frac{x^2}{2} + o(x^2))，(sqrt{1+2x} = 1 + x
  • frac{x^2}{2} + o(x^2))。
  • 步骤二：代入后分子化简为 (frac{3x^2}{2} + o(x^2))，分母为(x^2)，直接约分得极限值为(frac{3}{2})。

    • 方法总结：泰勒展开法在极限计算中具有普适性，需熟练掌握常见函数的展开式及精度控制。

    2. 微分中值定理证明题——构建辅助函数的思维路径

    例题（2017年第18题）：设函数(f(x))在([a,b])上连续，在((a,b))内可导，证明存在(xi in (a,b))，使得(f'(xi) = frac{f(b)-f(a)}{b-a} + frac{xi

  • a}{2})。

    • 解题思路：

  • 关键点：通过构造辅助函数将问题转化为罗尔定理的应用。
  • 辅助函数设计：令(F(x) = f(x)
  • frac{f(b)-f(a)}{b-a}x - frac{(x-a)^2}{2})，验证(F(a)=F(b))后，由罗尔定理得证。

    • 策略启示：中值定理证明题需掌握“构造法”与“逆向思维”，通过分析目标式结构反推辅助函数形式。

    三、备考策略建议：理论结合实践，优化复习路径

    基于真题解析结果，考生需从知识体系构建与实练两方面入手，制定科学备考计划：

    1. 知识体系化：建立“模块-题型-方法”三级框架

  • 将考点按模块分类（如微积分、线性代数），针对每个模块总结高频题型及对应解法。
  • 利用思维导图梳理知识脉络，避免知识点孤立。例如，将微分方程与积分应用结合，形成“问题链”。

    • 2. 训练精准化：强化真题模拟与错题归因

  • 以近十年真题为蓝本，分阶段进行限时训练，重点关注重复出错题型。
  • 建立错题本，标注错误原因（如计算失误、方法选择不当），定期复盘。

    • 3. 方法科学化：引入认知心理学理论提升效率

  • 间隔重复：根据艾宾浩斯遗忘曲线，定期回顾核心公式与解题模板。
  • 组块化学习：将复杂问题拆解为多个子步骤（如极限计算→泰勒展开→化简），降低认知负荷。

    • 以真题为镜，照见备考之道

    2017年考研数学二真题不仅是一份历史试卷，更是命题规律与复习方向的“指南针”。通过深度解析核心考点与典型题型，考生能够精准定位薄弱环节，优化复习策略。备考过程中，需坚持“理论为基、实战为王”的原则，将方法论的提炼与反复训练相结合，最终实现从“知识积累”到“能力跃迁”的跨越。面对未来挑战，唯有以真题为锚点，以方法为舟楫，方能在考场上从容应对，稳操胜券。